Hier wird folgende Gewichtsfunktion verwendet:
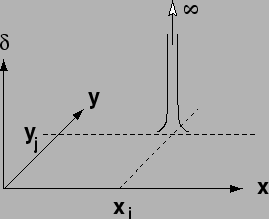
per Definition gilt:
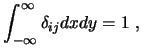
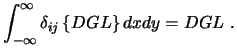
Die Finite-Differenzen-Methode versucht das Residuum an diskreten (endlich vielen) Stellen verschwinden zu lassen. Der Residuenverlauf zwischen den Kontrollpunkten bleibt unbeeinflußt, insbesondere können sich die Residuen zu einer von null verschiedenen Resultierenden aufsummieren, woraus erhebliche Kontinuitätsdefekte entstehen.
![\includegraphics*[width=6.0cm, angle=0]{Abb/bild0-6.eps}](img172.png)