Algebraische Gleichungen beinhalten die unbekannten Werte
von ![]() an den gewählten Gitterpunkten.
Die Herleitung einer Approximation erfordert Annahmen über
den Verlauf von
an den gewählten Gitterpunkten.
Die Herleitung einer Approximation erfordert Annahmen über
den Verlauf von ![]() zwischen den Gitterpunkten.
Das
zwischen den Gitterpunkten.
Das ![]() -''Profil'' kann ein einziger algebraischer Ausdruck für
das ganze Rechengebiet sein, z.B. eine Fourierreihe.
Eine solche Lösung hat sich jedoch als unpraktisch erwiesen.
Stattdessen werden wesentlich günstigere stückweise Profile
(Segmente) verwendet.
Dabei wird die Tatsache ausgenutzt, daß
der Wert von
-''Profil'' kann ein einziger algebraischer Ausdruck für
das ganze Rechengebiet sein, z.B. eine Fourierreihe.
Eine solche Lösung hat sich jedoch als unpraktisch erwiesen.
Stattdessen werden wesentlich günstigere stückweise Profile
(Segmente) verwendet.
Dabei wird die Tatsache ausgenutzt, daß
der Wert von ![]() an einem Punkt nur die
an einem Punkt nur die
![]() -Verteilung in seiner unmittelbaren Umgebung beeinflußt.
Jedes Segment beschreibt die
Variation von
-Verteilung in seiner unmittelbaren Umgebung beeinflußt.
Jedes Segment beschreibt die
Variation von ![]() über ein kleines Gebiet in Abhängigkeit von
benachbarten
über ein kleines Gebiet in Abhängigkeit von
benachbarten ![]() -Werten.
-Werten.
Alle Verfahren sollen zunächst auf eindimensionale Probleme
beschränkt betrachtet werden:
Die Diskretisierungsgleichung ist eine algebraische Beziehung zur
Verbindung der ![]() -Werte für eine Gruppe von Gitterpunkten.
Für große Punktzahlen ist die Lösung der Diskretisierungsgleichung
gleich der exakten Lösung der Differentialgleichung.
-Werte für eine Gruppe von Gitterpunkten.
Für große Punktzahlen ist die Lösung der Diskretisierungsgleichung
gleich der exakten Lösung der Differentialgleichung.
Die möglichen Diskretisierungsgleichungen sind nicht einzigartig,
sondern es lassen sich sehr unterschiedliche Verfahren ableiten.
Die Typenvielfalt resultiert aus Unterschieden in den
Profilannahmen und in der Methode der Herleitung:
Im Prinzip sind sich die Methoden sehr ähnlich. Der Verlauf
der Lösung zwischen den Gitterpunkten wird im allgemeinen auf
dieselbe Weise durch bedarfsweise mehr oder weniger
hochgradige Polynome angenähert.
Die Amplituden (oder Stützwerte)
![]() für diesen
Polynomansatz ergeben sich aus Kollokation:
für diesen
Polynomansatz ergeben sich aus Kollokation:
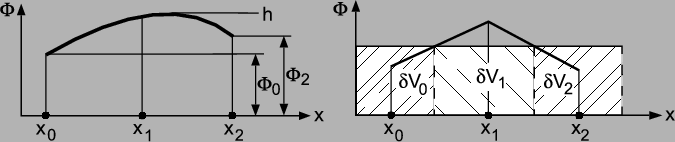 |
Am Beispiel der Kontinuitätsgleichung (3.1) soll dieser Unterschied mathematisch beschrieben werden:
Gesucht ist der Verlauf der Flüsse ''![]() '' und ''
'' und ''![]() '' als
Funktion von
'' als
Funktion von ![]() und
und ![]() . (Hierzu ist selbstverständlich noch
eine weitere Zwangsbedingung, z.B. die Impulsgleichung, erforderlich.)
. (Hierzu ist selbstverständlich noch
eine weitere Zwangsbedingung, z.B. die Impulsgleichung, erforderlich.)
Die (exakte) Lösung erfüllt die Differentialgleichung überall, so daß wir hierfür auch die ''Integro-Differentialgleichung''
![$\displaystyle \int\limits_{\delta V} \left[ \partial x(\rho u) + \partial y(\rho v) \right] dx dy \underbrace{dz}_{=1} \ ,$](img155.png) |
(3.2) |
notieren können. Für die exakte Lösung ist die Integro-Differentialgleichung der Differentialgleichung äquivalent.
![]() Die Lösungen der beiden Ausdrücke entsprechen
sich auch für beliebige Unterteilungen
Die Lösungen der beiden Ausdrücke entsprechen
sich auch für beliebige Unterteilungen
Eine weitere, sicherlich ebenso richtige Integro-Differentialgleichungsformulierung lautet:
Hierbei wird das Integral über die Differentialgleichung zusätzlich noch gewichtet. Diese Betrachtungen führen auf die Methoden der gewichteten Residuen.