Betrachten wir ein
allgemeines, krummliniges Koordinatensystem mit den Koordinatenlinien
![]() , das sich an den
lokalen Gitterlinien ausrichtet.
Im Zusammenhang mit der numerischen Behandlung der Bilanzgleichungen
sind nun eine Reihe von Transformationen notwendig.
Zum Verständnis der Transformationsbeziehungen soll zuerst auf die
Eigenschaften des Koordinatensystems eingegangen werden.
, das sich an den
lokalen Gitterlinien ausrichtet.
Im Zusammenhang mit der numerischen Behandlung der Bilanzgleichungen
sind nun eine Reihe von Transformationen notwendig.
Zum Verständnis der Transformationsbeziehungen soll zuerst auf die
Eigenschaften des Koordinatensystems eingegangen werden.
Der Basisvektor
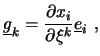
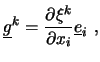
Der Transformationszusammenhang zwischen ![]() und
und ![]() wird durch
mehrere unterschiedliche Metrikterme beschrieben. Von Bedeutung
ist vor allem die Transformationsmatrix
wird durch
mehrere unterschiedliche Metrikterme beschrieben. Von Bedeutung
ist vor allem die Transformationsmatrix
![]() (Jakobi-Matrix) und die Funktionaldeterminante
(Jakobi-Matrix) und die Funktionaldeterminante ![]() der Transformation
des kartesischen Koordinatensystems in das lokale System des
Rechengitters.
der Transformation
des kartesischen Koordinatensystems in das lokale System des
Rechengitters.
![]() bildet dabei die Matrix
der kovarianten Metrikkoeffizienten:
bildet dabei die Matrix
der kovarianten Metrikkoeffizienten:
![$\displaystyle \qquad \underline{\underline{J}} = \frac{\partial (x_1, x_2, x_3)...
...eta} & y_{,\zeta} \\ z_{,\xi} & z_{,\eta} & z_{,\zeta} \end{array} \right] \ ,$](img945.png) |
(7.4) |
oder im zweidimensionalen Fall:
![$\displaystyle \left[ \begin{array}{cc} x_{,\xi} & x_{,\eta} \\ y_{,\xi} & y_{,\eta} \end{array} \right] = x_{,\xi} y_{,\eta} - x_{,\eta} y_{,\xi} \ .$](img948.png) |
(7.5) |
Im folgenden soll die Herleitung wegen der besseren Übersichtlichkeit
komplett auf zweidimensionale Fälle beschränkt bleiben.
Mit (7.3) und Inversion ergeben sich die erforderlichen
Transformationsbeziehungen für die Metrikterme:
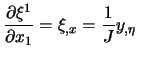 |
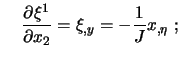 |
||
| (7.6) | |||
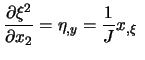 |
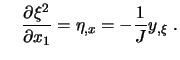 |
Die Geometrie wird im Allgemeinen in Form der Koordinaten
![]() und
und ![]() der Kontrollvolumenzentren und der Gitterknotenpunkte
bzw. Kontrollvolumenecken gespeichert (siehe Abbildung 53).
der Kontrollvolumenzentren und der Gitterknotenpunkte
bzw. Kontrollvolumenecken gespeichert (siehe Abbildung 53).
Üblicherweise wird der frei wählbare Skalierungsfaktor des natürlichen Koordinatensystems so gewählt, daß die Längen über ein Kontrollvolumen gerade ''1'' ergeben. Die Metrikterme können dann am ''east'' Rand über
berechnet werden.
Ausgehend von einer beliebigen, zweidimensionalen Transportgleichung (5.38) soll nun die Diskretisierung in einem allgemeinen, krummlinigen Koordinatensystem abgeleitet werden. Die Integration der Differentialgleichung
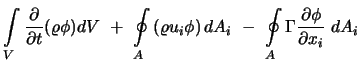 |
 |
(7.8) |
über ein Kontrollvolumen ![]() bzw. die Kontrollvolumenoberflächen
bzw. die Kontrollvolumenoberflächen
![]() führt dann im krummlinigen System auf
führt dann im krummlinigen System auf
![$\displaystyle \left.\frac{\partial (\varrho \phi)}{\partial t} \Delta V \right\...
...lta A \ \phi \right]_w^e
+ \left[ \varrho u_i n_i \ \Delta A \ \phi \right]_s^n$](img962.png) |
|||
![$\displaystyle - \left[ \Gamma \frac{\partial \xi^k}{\partial x_i}
\frac{\partia...
...{\partial x_i}
\frac{\partial \phi }{\partial \xi^k} \ n_i \Delta A \right]_s^n$](img963.png) |
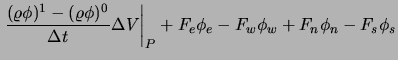 |
|||
![$\displaystyle - \Gamma_e \ \Delta A_e \left[ \frac{\partial \xi^k}{\partial x_i...
...tial \xi^k}{\partial x_i}
\frac{\partial \phi }{\partial \xi^k} \ n_i \right]_w$](img966.png) |
|||
![$\displaystyle - \Gamma_n \ \Delta A_n \left[ \frac{\partial \xi^k}{\partial x_i...
...tial \xi^k}{\partial x_i}
\frac{\partial \phi }{\partial \xi^k} \ n_i \right]_s$](img967.png) |
(7.9) |
Dabei sind ![]() die Komponenten des normierten Flächennormalenvektors
einer Kontrollvolumenoberfläche und
die Komponenten des normierten Flächennormalenvektors
einer Kontrollvolumenoberfläche und ![]() die Größe dieser
Fläche. Wie aus Abbildung 53 zu entnehmen ist, ergibt sich
der hierbei auftauchende Ausdruck
die Größe dieser
Fläche. Wie aus Abbildung 53 zu entnehmen ist, ergibt sich
der hierbei auftauchende Ausdruck
![]() bzw.
die analog an den übrigen Kontrollvolumenseiten auftretenden Terme zu:
bzw.
die analog an den übrigen Kontrollvolumenseiten auftretenden Terme zu: