Transfinite Interpolation bei 3D-Gittern

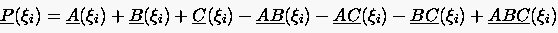
Bei der Erweiterung der zweidimensionalen Interpolation auf den 3D-Fall werden drei oberflächenkonforme, krummlinige Koordinaten $$_i; i=1,2,3 definiert. Dies bedeutet, daß jede Oberfläche identisch ist mit einer Koordinatenfläche, die ihrerseits durch zwei Koordinatenlinienscharen aufgespannt wird und auf der die jeweils dritte Koordinate konstant ist (Abb. 78). Die konsequente Konstruktion der Transfiniten Interpolation nimmt dann die folgende komplexe Form an:

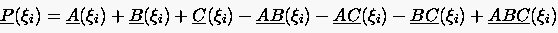(6.111)

Abbildung 78: 3D Transfinite Interpolation

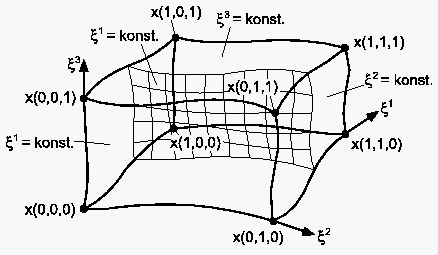Die einzelnen Terme in der obigen Gleichung behalten ihre Bedeutung. Die Ausführungen für Flächen werden hier lediglich auf die drei Raumkoordinaten $$_i erweitert. Dementsprechend kommt zu den beiden Scherungstransformationen $A$ und $B$ eine dritte Transformation $C$ hinzu. Die einfache Tensor-Produkt-Transformation $A\; B$ wird ebenfalls um zwei weitere Transformationen $A\; C$ und $B\; C$ ergänzt, da ja der 3D-Raum durch drei unabhängige Flächenscharen aufgespannt wird, auf denen jeweils eine Raumkoordinate $$_i konstant ist. Auf diese Weise wird jede Koordinatenfläche wie in einer 2D Transfiniten Interpolation behandelt, und die Randkurven einer jeden Koordinatenfläche verlaufen genau in den Berandungsflächen des betrachteten Raumes. In ihrer Gesamtheit bilden dann die Koordinatenflächen ein Netz auf den Randflächen.

Die doppelte Tensor-Produkt-Transformation $A\; B\; C$ ist schließlich nötig, um eine Korrektur der Transformation, wie sie die ersten sechs Terme in Gleichung (6.111) vermitteln, in der Weise vorzunehmen, daß die acht Eckpunkte des Gebiets durch Gleichung (6.111) reproduziert werden.

Die explizite Form der Terme in Gleichung (6.111) wird im folgenden vorgegeben:

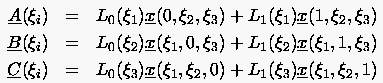(6.112)

Die einfachen Tensor-Produkt-Transformationen sind kommutativ und folgen durch sukzessive Anwendung von $A$ auf $B$, von $A$ auf $C$ und von $B$ auf $C$.

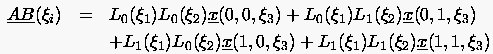(6.113)

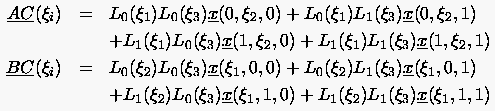(6.114)

Die doppelte Tensor-Produkt-Transformation ist ebenso wie die einfache kommutativ. $A\; B\; C$ kann dann beispielsweise durch Anwendung von $A$ auf das einfache Tensorprodukt $B\; C$ gebildet werden.

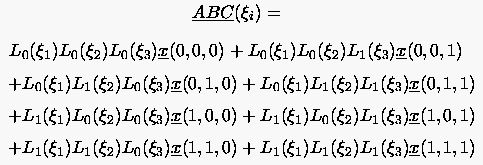(6.115)

Diese Gleichung kann auch als trilineare Interpolation zwischen den acht Eckpunkten $x\; (0,0,0)$, $x\; (0,0,1)$, $x\; (0,1,0)$, $x\; (0,1,1)$, $x\; (1,0,0)$, $x\; (1,0,1)$, $x\; (1,1,0)$ und $x\; (1,1,1)$ des betrachteten räumlichen Gebietes verstanden werden.