Verteilung auf einer Kurve

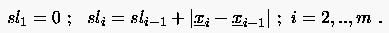
Mathematisch gesehen suchen wir eine geeignete Verteilung des Kurvenparameters
$$(G_i) , i = 1 ,..,IG , so daß die entsprechende Punkteverteilung $G$_i auf der Kurve bestimmten Anforderungen, wie z.B. Verdichtung in bestimmten Bereichen, genügt.

Um bessere Kontrolle zu erlangen, basiert die Bestimmung der Verteilung meist auf der auf die Stützpunkte bezogenen, normierten resultierenden Sekantenlänge $s$. Es ist zunächst die Abbildungsvorschrift zwischen dem Längenmaß $s$ und dem Kurvenparameter $$ zu bestimmen. Dabei wird die resultierende Sekantenlänge $sl$_i für alle Stützpunkte $S$_i einer Kurve berechnet:

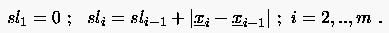(6.96)

Es folgt dann die Normierung auf die gesamte Länge:

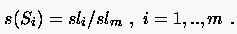(6.97)

Da jeder Stützpunkt einen Wert des Kurvenparameters hat, kann die Beziehung von $s$ und $$ z.B. durch lineare Interpolation festgelegt werden.

Die Bestimmung der Verteilungsfunktion $s(G$_i) der Punkte geschieht unabhängig davon nach den gestellten Anforderungen.

Schließlich wird die Verteilungsfunktion $s(G$_i) zurück auf den Kurvenparameter $$(G_i) abgebildet und damit sind die zu verteilenden Punkte bestimmt.

Abbildung 65: $s-$(S_i)- und $s-G$_i- Diagramm und die Abbildung von $$(G_i)

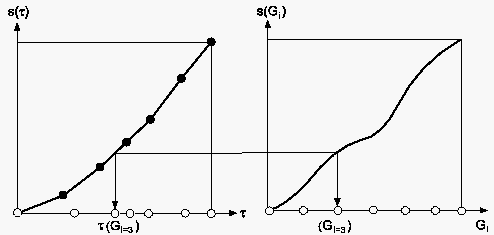Die Verteilungsfunktion $s(G$_i) muß natürlich eine monoton steigende Funktion sein. Ihre Steigung legt in etwa die auf das Längenmaß bezogene Schrittweite fest.

Ihre 1. Ableitung sollte nach Möglichkeit stetig verlaufen. Ein Knick in der Verteilungsfunktion bedeutet eine unstetige Änderung in der Schrittweite.

Die einfachste Verteilungsfunktion ist eine Gerade. Sie erzeugt eine beinahe äquidistante Punkteverteilung.

Eine weitere häufig verwendete Verteilungsfunktion ist die exponentielle Funktion
(IG: Anzahl der zu verteilenden Punkte):

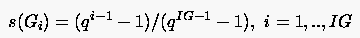(6.98)

Sie wird häufig verwendet, um die Gitterpunkteverteilung zwischen dem körpernahen Bereich und dem Fernfeld zu bestimmen. Der Parameter $q$ gibt das Verhältnis zweier aufeinander folgender Punkteabstände an.

Eine ähnliche Funktion, die das Verhältnis der maximalen und der minimalen Punkteabstände festlegt, hat folgende Gestalt:

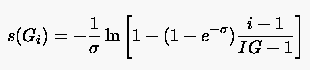(6.99)

Das Verhältnis wird durch $e$ bestimmt.

Um in bestimmten Bereichen die Verteilung der Gitterpunkte zu verdichten, ist folgende Verteilungsfunktion geeignet:

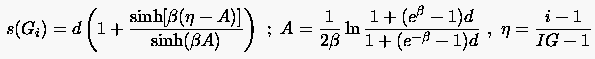(6.100)

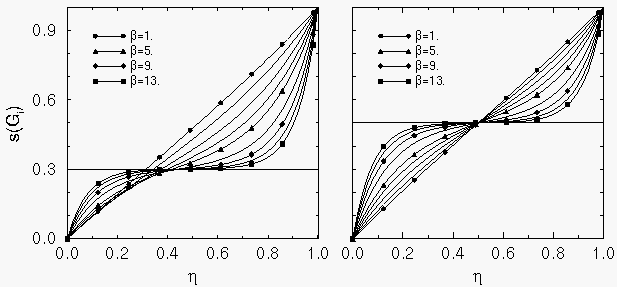
Mit der obigen Funktion wird die Punkteverteilung um $s=d$ verdichtet. Die Stärke der Verdichtung bestimmt der Parameter $$. Abbildung 66 zeigt den Verlauf dieser Funktion bei einigen unterschiedlich gewählten Parametern $d$ und $$ .

Abbildung 66: Die Verteilungsfunktion zur gezielten Verdichtung der Punkteverteilung, Parametervariation in Formel (6.100), links: $d=0.3$, $$ rechts: $d=0.5$

Bei komplexen CFD-Problemen ist es meistens notwendig, mehrere Bereiche um den Körper herum (Hinterkante, Nase, Verdichtungsstoß ...) mit dichterer Verteilung der Gitterpunkte zu versehen. Dies mit einer einzigen analytischen Funktion zu erreichen, ist mathematisch sehr aufwendig und auch nicht notwendig. Hier kann die Verteilungsfunktion intervallweise definiert werden.

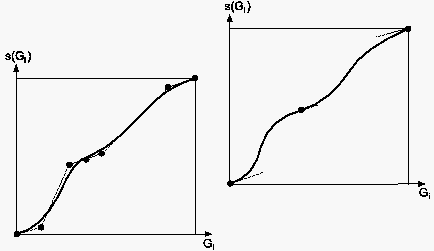
Um den Knick im Verlauf der gesamten Verteilungsfunktion zu vermeiden, können die im letzten Abschnitt beschriebene intervallweise Hermitesche Interpolation oder die Bézier-Spline-Approximation herangezogen werden, da sie geeignet sind, um eine glatte Verteilungsfunktion zu generieren. Dabei kann jeder gewünschte Bereich zunächst durch Funktionswerte oder ihre Ableitungen, was dem Abstand zwischen den Punkten entspricht, fixiert werden. Die Verteilungsfunktion geht dann entweder aus der Bézier-Spline-Approximation aller fixierten Funktionswerte oder intervallweiser Hermitescher Interpolation hervor.

Wenn interaktive Arbeitsmöglichkeiten vorhanden sind, kann damit die gewünschte Verteilungsfunktion sehr schnell generiert werden.

Abbildung 67: Verteilungsfunktion mittels Bézier-Spline oder Hermitescher Interpolation