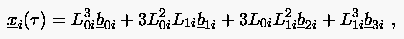
Der kubische Bézier-Spline zur Approximation von Kurven

Der kubische Bézier-Spline verwendet Polynome 3. Grades und approximiert den Kurvenverlauf durch vier sogenannte ''Bézier-Punkte'' in jedem Intervall.

Seien vier Bézier-Punkte $B$_ki (b _ki ; k = 0,1,2,3) im Intervall $i\; ($ Element von [ _i , _i+1 ] ) gegeben, dann wird der Kurvenverlauf zwischen den Punkten $B$_0i und $B$_3i wie folgt approximiert:

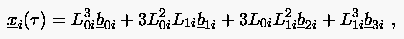(6.83)

mit den Lagrangeschen Polynomen 1. Ordnung $L$_0i, L_1i :

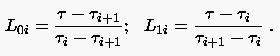
Das Resultat dieser Approximation ist, daß die Kurve durch die Punkte $B$_0i ( = _i ) und $B$_3i ( = _i+1 ) läuft und die Tangenten an den Stellen $$= _i bzw. $$= _i+1 in die gleiche Richtung wie zeigen.

Abbildung 63: Bézier-Punkte und kubischer Bézier-Spline

Das läßt sich leicht durch die Bildung der 1. Ableitung der Kurve zeigen:

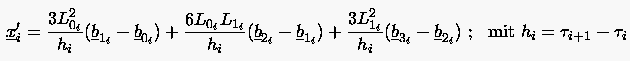(6.84)

Daraus folgt:

Die 2. Ableitung lautet:

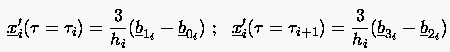
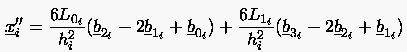(6.85)

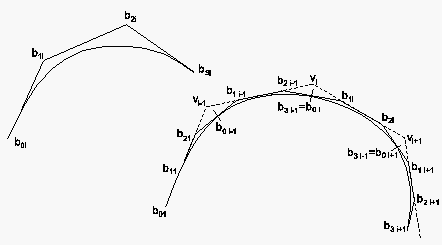
Verlangt wird hier, wie bei der kubischen Spline-Interpolation, daß die Kurve sowie ihre 1. und 2. Ableitung an den Intervallgrenzen $($= _i; i=2,..,n-1) stetig sind. Betrachten wir nun 2 Intervalle, i-1 und i:

Die 3 Bedingungen führen auf folgende Gleichung:

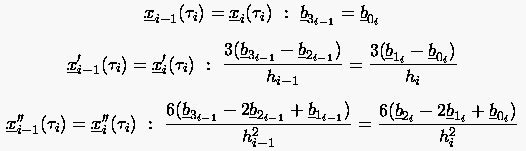
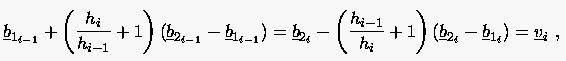(6.86)

was nichts anderes bedeutet, als daß die Punkte $B$1_i-1 , B₁2_i-1 und $B$1_i , B 2_i in einem bestimmten Verhältnis zum Schnittpunkt $V$_i (v _i ) der Verlängerungslinien von den Strecken 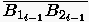und 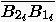liegen müssen. Das Verhältnis hängt von der Wahl des Kurvenparameters $$ ab.

Bei der Bézier-Spline-Approximation werden normalerweise die Schnittpunkte $V$_i (v _i; i=1,..,n ) , die auch Gewichtspunkte genannt werden, vorgegeben. Daraus werden zunächst die Bézier-Punkte $B$_1i, B_2i nach der Beziehung (6.86):

bestimmt:

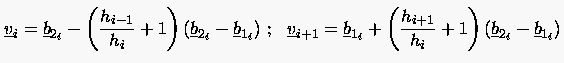
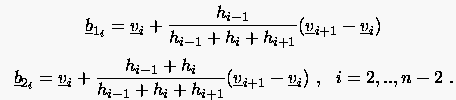(6.87)

Bei der offenen Kurve werden die Bézier-Punkte $B$0_i=1 und $B$3_i=n-1 mit den Gewichtspunkten $V$₁ und $V$_n gleichgesetzt. Die Positionen von $B$1_i=1, B₁2_i=1 und von $B$1_i=n-1, B₁2_i=n-1 bestimmt man aus den Formeln (6.86) und der Vorgabe von $x\; \text{'}\; ($₁ ) , x ' ( _n ) oder $x\; \text{'}\text{'}($₁ ) , x ''( _n ) . Z.B. gilt für $x\; \text{'}\text{'}($₁ ) = 0 (dies wird zusammen mit $x\; \text{'}\text{'}($_n ) = 0 meistens für eine offene Kurve eingesetzt):

oder

Hinweis:

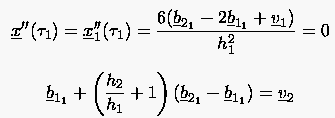
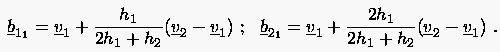
Wenn man in den Gleichungen (6.87) formal $i\; =\; 1$ und $h$₀ = h₁ einsetzt, ergeben sich die gleichen Formeln wie oben. Analog gilt es für $x\; \text{'}\text{'}($_n ) = 0 mit $i\; =\; n\; -1$ und $h$_n = h_n-1 :

Für eine geschlossene Kurve werden die Bézier-Punkte in dem Intervall $1\; ($₁ < < ₂ ) bzw. $n\; ($_n < < _n+1 ) genauso erzeugt wie in dem inneren Intervall, indem man in der Gleichungen (6.87) für $i\; =\; 1$ $h$₀ durch $h$_n und für $i\; =\; n$ $h$_n+1 durch $h$₁ und $v$_n+1 durch $v$₁ ersetzt:

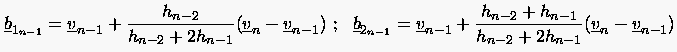
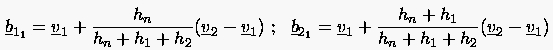(6.88)

bzw.

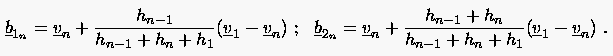(6.89)

Danach können die Punkte $B$_0i bzw. $B$3_i-1 nach der Formel:

oder

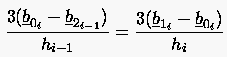
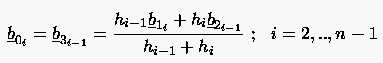(6.90)

berechnet werden. Bei einer geschlossenen Kurve gilt obige Gleichung zusätzlich noch für $i\; =\; n$: Die Positionen von $B$₀₁ bzw. $B$_3n werden mit der folgenden Formel bestimmt:

Durch die Anwendung der Bézier-Approximationsformel (6.83) in jedem Intervall ($i=1,..,n-1$ für die offene und $i\; =\; 1,\; ..\; ,\; n$ für die geschlossene Kurve) entsteht schließlich eine zweimal stetig differenzierbare Kurve. Ihr Verlauf approximiert die exakte Kurve, die durch die Punkte $V$_i geht.

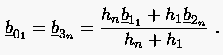
Der Vorteil der Bézier-Spline-Interpolation liegt zunächst darin, daß aus den gegebenen Gewichtspunkten die Bézier-Punkte für jedes Intervall direkt bestimmt werden können, womit die gesamte Approximationskurve festgelegt ist. Außerdem beeinflußt die Änderung oder das Hinzufügen von Gewichtspunkten nur wenige lokale Kurvensegmente.