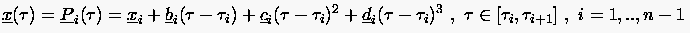
Die Kurve in einer Ebene kann mit der im vorigen Abschnitt beschriebenen Methode interpoliert werden, wenn wir die Funktion durch und die unabhängige Variable durch ersetzen. Diese Methode setzt leider den monotonen Anstieg von x voraus und kann z.B. eine geschlossene Kurve nicht interpolieren. Eine allgemeinere Methode, mit der man auch die Kurve im 3D-Raum interpolieren kann, ist die sogenannte ''Parameter-Spline-Interpolation''.
Hier werden die Komponenten der Kurvenkoordinaten einzeln mit Splinefunktionen interpoliert. Der gewonnene Kurvenverlauf ist somit zweimal stetig nach dem Kurvenparameter differenzierbar, was eine gute Glattheit verspricht.
Von der zu interpolierenden Kurve seien die Ortsvektoren an den n Stützstellen gegeben. Dann gilt:
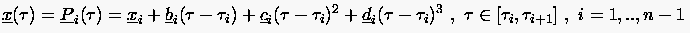 |
(6.73) |
Die Komponenten der Koeffizienten werden nach den Formeln (6.65) bis (6.67) berechnet, indem man jeweils die Komponenten der Stützpunkte als Stützwerte der Funktion einsetzt.
Als Kurvenparameter kann entweder der Laufindex,
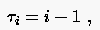 |
(6.74) |
die resultierende Sekantenlänge
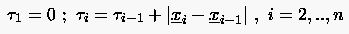 |
(6.75) |
oder eine beliebige monoton steigende Funtion verwendet werden.
Für eine geschlossene Kurve wird der Punkt zusätzlich als definiert.
Anstelle der Schließungsgleichung an den Rändern verlangen wir wiederum die zweimal stetige Differenzierbarkeit auch an dem Punkt
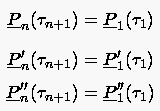
:
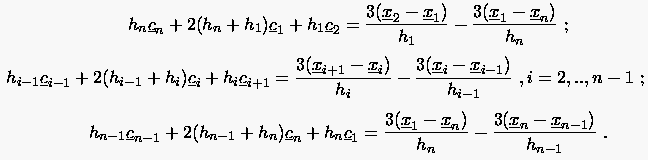 |
(6.76) |
:
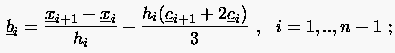 |
(6.77) |
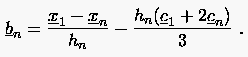 |
:
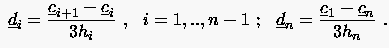 |
(6.78) |
Die Kurve wird dann aus den folgenden Segmenten zusammengesetzt:
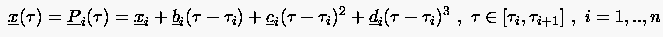 |
(6.79) |
Man kann hier auch die alternative Methode (vgl. vorherigen Abschnitt) einsetzen. Es wird dann die Ableitung des Ortsvektors nach dem Kurvenparameter gesucht. zeigt in die gleiche Richtung wie die Tangente der interpolierten Kurve.
Analog zur Gleichung (6.71) bestimmt man aus dem folgenden Gleichungssystem:
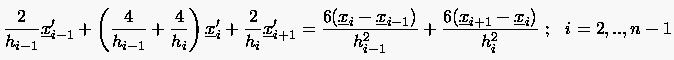 |
(6.80) |
mit der Schließungsbeziehung:
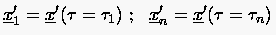
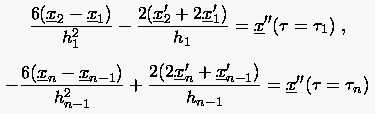
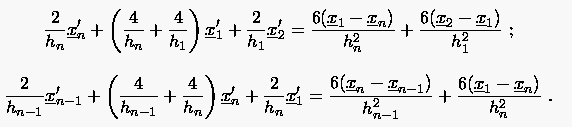 |
(6.81) |
Es ist zu beachten, daß hier 3 Gleichungssysteme zu lösen sind.
Der Kurvenverlauf der einzelnen Intervalle ergibt sich aus:
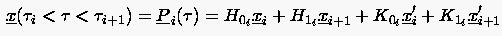 |
(6.82) |
mit für die offene und für die geschlossene Kurve.