



Next: Formulierungsmethoden
Up: Klassifizierung partieller Differentialgleichungen (PDG)
Previous: Beispiel: Charakteristikenverfahren
Bei der Integration partieller Dgl. fallen (ähnlich den
Integrationskonstanten für gewöhnliche Dgl.) Funktionen an.
Eine geschlossene Lösung erhält man nur sofern diese durch
zusätzliche Bedingungen bestimmbar werden. Hierbei
unterscheidet man zwischen Anfangs- und Randbedingungen.
- Anfangsbedingungen
- sind Vorschriften an den Wert der abhängigen Variablen im Ausgangszustand.
- Randbedingungen
- sind Vorschriften an den Wert der abhängigen Variablen oder ihrer Ableitung auf dem Bereichsrand.
Folgende Randbedingungen sind namentlich bekannt:
- 1. Dirichletbindung:
- Der Wert der anhängingen Variablen
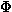 ist entlang des Bereichsrandes gegeben.
ist entlang des Bereichsrandes gegeben.
- 2. Neumannbindung:
- Die Normalenableitung der unabhängigen Variablen
entlang des Randes ist vorgegeben.
- 3. Gemischte (Cauchy-)
Randbedingungen:
- An einem Teil der Berandung sind
Dirichletrandbedingungen gegeben, an einem anderen Neumannbedingungen.
- 4. Robinbedingung:
- Hiermit sind Linearkombinationen von Dirichlet-
und Neumannbedingungen gemeint.
Achtung: Reine Gradientenbedingungen können das Problem nicht
eindeutig lösen, da das Niveau nicht festgelegt ist.




Next: Formulierungsmethoden
Up: Klassifizierung partieller Differentialgleichungen (PDG)
Previous: Beispiel: Charakteristikenverfahren
Benjamin Gilde
Sat Dec 16 15:24:45 CET 2000
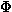 ist entlang des Bereichsrandes gegeben.
ist entlang des Bereichsrandes gegeben.
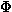 ist entlang des Bereichsrandes gegeben.
ist entlang des Bereichsrandes gegeben.