Die Lagrangesche und Hermitesche Interpolation von Kurven

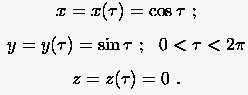
Eine Kurve im physikalischen Raum ist in jedem Punkt durch den Ortsvektor $x$ in der Parameterdarstellung $x\; ($) definiert. Dabei ist $$ der Kurvenparameter, der entlang der Kurve monoton ansteigt, und $x$ ist durch die drei kartesischen Koordinaten $x$_i des entsprechenden Kurvenpunktes bestimmt. Ein Einheitskreis in der Ebene (z = 0) kann z.B. wie folgt dargestellt werden:

Oft ist nur eine endliche Anzahl von Punkten $x\; ($_k ) für diskrete Werte $$_k (k = 0, ..., n ) des Kurvenparameters gegeben, und der Verlauf der Kurve zwischen diesen Stützpunkten wird durch entsprechende Interpolationspolynome approximiert. Ist $n+1$ die Anzahl der gegebenen Punkte, dann kann ein Polynom $P$_L ( ) vom Grade $n$ konstruiert werden, das genau durch diese Punkte läuft. Die allgemeine Form von $P$_L ( ) ist durch die Lagrangesche Interpolationsformel

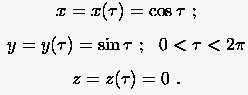
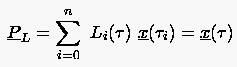(6.56)

gegeben, mit den Lagrange-Polynomen

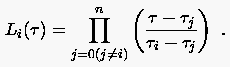(6.57)

Man realisiert leicht, da\3 Gleichung (6.56) für $$_i = die gegebenen Punkte $x\; ($_i ) reproduziert.

Eine alternative Methode zur Lagrangeschen Interpolation ist die Hermitesche Interpolation. In ihr wird zusätzlich zu den diskreten Kurvenpunkten auch die Steigung der Kurve in diesen Punkten vorgeschrieben. Die Steigung im Punkte $x\; ($_i ) ist ihrerseits durch die partielle Ableitung des Ortsvektors nach dem Kurvenparameter und damit durch $x\; \text{'}\; ($_i ) bestimmt.

Die allgemeine Form der Hermiteschen Interpolation lautet:

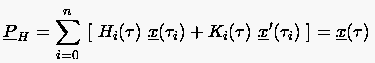(6.58)

mit den Hermiteschen Polynomen

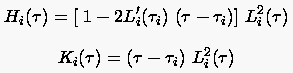(6.59)

Obwohl die Hermitesche Interpolation Vorteile aufweist, ist sie aufgrund ihrer Sensitivität gegenüber leichten Änderungen in den Steigungswerten $x\; \text{'}\; ($_i ) nur sehr schwierig zu handhaben.

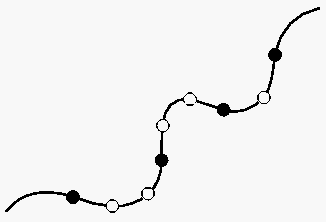
Der Hauptnachteil sowohl der Lagrangeschen als auch Hermiteschen Interpolation liegt letztlich darin, da\3 beide bei Verwendung mehrerer Punkte zu starken Oszillationen neigen (Abb. 61).

Abbildung 61: Kurve, die nach Lagrange oder Hermite gemäß Gleichung (6.56) bzw. Gleichung (6.58) interpoliert ist; $$schwarzer Punkt vorgegebene Kurvenpunkte; $o$ interpolierte Kurvenpunkte; -- oszillierender Verlauf der Interpolationskurve.

Ein wichtiger Spezialfall, der in der algebraischen Gittergenerierung eine große Rolle spielt, folgt aus Gleichung (6.56) bzw. Gleichung (6.58) für $n=1$, d.h. wenn nur der linke und rechte Randpunkt in die Interpolation eingehen. In diesem Fall können natürlich keine Oszillationen auftreten. Hier gilt allgemein:

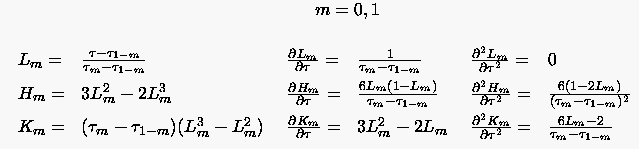(6.60)

Unter der Annahme, daß 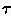₀ = 0 und 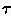₁ = 1 ist, folgt dann für die Lagrangesche Interpolation

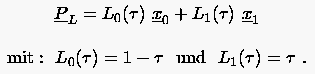(6.61)

Gleichung (6.60) wird auch als Scherungstransformation bezeichnet. Für die Hermitesche Interpolation gilt analog

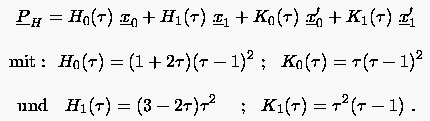(6.62)

Abbildung 62: Funktionsverläufe der Lagrangeschen bzw. Hermiteschen Polynome für zwei Stützstelle

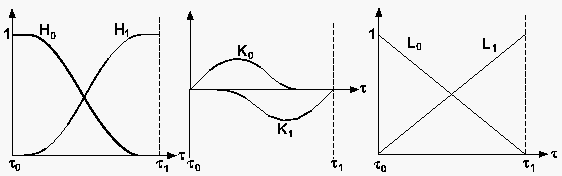In Abb. 62 sind die Verläufe der Lagrangeschen bzw. Hermiteschen Polynome dargestellt. Das Interpolationspolynom kann als Einflu\3faktor des einzelnen Stützwertes auf den gesamten Funktionsverlauf interpretiert werden.

Der Kurvenparameter $$ kann seinerseits eine beliebige Funktion einer neuen Variablen $$ sein, wodurch entsprechend dem gewählten funktionalen Zusammenhang die Punkteverteilung auf der Interpolationskurve manipuliert werden kann. $$() wird deshalb auch als Verteilungs- oder Streckungsfunktion bezeichnet.