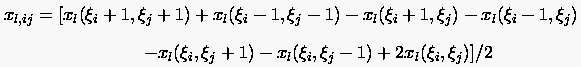
Analog zur einseitigen Differenzenapproximation für die ersten Ableitungen lassen sich für die gemischten zweiten Ableitungen die folgenden ''schiefen'' upwind-Approximationen formulieren:
Wenn :
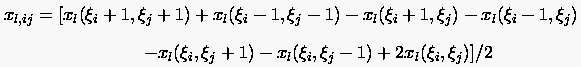 |
(6.137) |
Wenn :
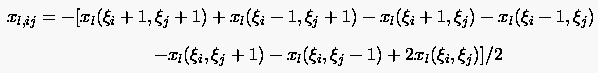 |
(6.138) |
Auch hier lassen sich die Gleichungen (6.132), (6.137) und (6.138) unter Einführung des Parameters zusammenfassen:
 |
(6.139) |
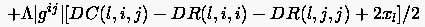 |
mit
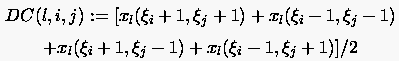 |
(6.140) |
Im Falle , wird zu null gesetzt, und es folgt die zentrale Approximation. Wenn ist, dann liefert ebenfalls wieder die zentrale Approximation, jedoch ist in diesem Fall die ''schiefe'' Approximation sinnvoller
Einsetzen der Gleichungen (6.135) und (6.139) in Gleichung (6.130) liefert schließlich die finite Differenzenapproximation der elliptischen Gittergenerierung im Punkt
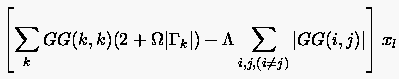 |
(6.141) |
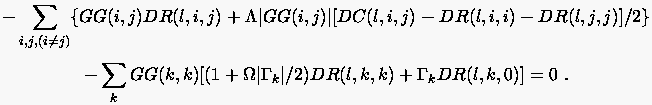
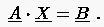
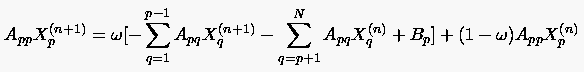 |
(6.142) |
Der obere Index bezeichnet die Iterationsstufe des SOR-Verfahrens. Die Folge aller inneren Punkte des Rechengebiets, die nach einer bestimmten Reihenfolge in dem eindimensionalen Array abgespeichert werden, ist durch den unteren Zählindex gekennzeichnet. ist der Relaxationsfaktor. Mit reduziert sich das SOR-Verfahren auf das Gauß-Seidel-Verfahren, während dieses im Fall bzw. durch Über- bzw. Unterrelaxation beschleunigt wird. Gemäß der Beziehung (6.142) werden nun alle nacheinander berechnet, wobei bereits ermittelte Werte für direkt in die Auswertung der rechten Seiten einfließen.
Unter Einführung des Zwischenwertes läßt sich das Auflösen der Gleichung (6.141) mit dem SOR-Verfahren in der kompakten Form schreiben:
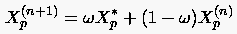 |
(6.143) |
mit
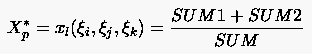
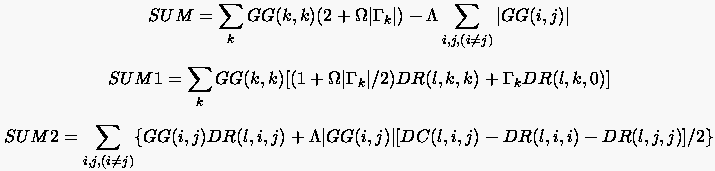
Entscheidend für das Konvergenzverhalten des SOR-Verfahrens ist die optimale Bestimmung des Relaxationsfaktors , auf dessen exakte Herleitung aufgrund der Komplexität hier nicht näher eingegangen werden kann. Dazu sei zunächst auf numerisches Experimentieren verwiesen.