![\includegraphics*[width=11cm, angle=0]{Abb/fvm1_1.eps}](img47.png)
|
Betrachtet werden die Flüsse einer beliebigen Größe an den Grenzen eines Volumenelements:
![]() : Fluß in
: Fluß in ![]() -Richtung = Strom der Größe pro Flächeneinheit.
-Richtung = Strom der Größe pro Flächeneinheit.
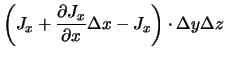 |
|||
| (2.7) | |||
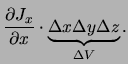 |
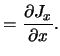 |
(2.8) |
Bei Betrachtung aller drei Raumrichtungen ![]() :
:
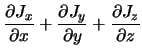 |
(2.9) | ||
Das Finite-Volumen-Verfahren basiert auf einer Bilanz über ein sogenanntes
Kontrollvolumen.
Die differentielle Form einer allgemeinen Bilanz lautet damit: 45
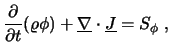 |
(2.10) |
bzw.
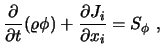 |
(2.11) |
mit den Flüssen
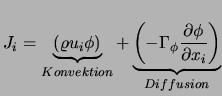 |
(2.12) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ein allgemeiner Diffusionskoeffizient (auch: Leitfähigkeit) | |
| Quellterm; Erzeugungsrate pro Volumeneinheit |
Es folgt die allgemeine differentielle Form der
Transportgleichung:
![]() kann stehen für
kann stehen für
Die Bilanzgleichungen für unterschiedliche Größen lassen sich alle in beiden oben erwähnten Formen (2.5, 2.13) darstellen. Sie drücken ein Erhaltungsprinzip aus.
Im allgemeinen ist ![]() eine Größe pro Masseneinheit.
Die Terme der Differentialgleichung sind Größen pro Volumen und pro
Zeiteinheit.
eine Größe pro Masseneinheit.
Die Terme der Differentialgleichung sind Größen pro Volumen und pro
Zeiteinheit.
| Sei | massenbezogene Größe | |
| (Dichte) Masse der Mischung pro Volumeneinheit, | ||
| dann |
|
Größe pro Volumeneinheit |
|
|
Änderung pro Volumen- und Zeiteinheit. |
Die Anwendung des Transporttheorems (2.4) auf die
Bilanzen für Impuls, Masse und Energie ergibt die entsprechenden
Transport- bzw. Erhaltungsgleichungen.