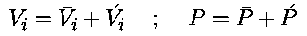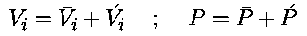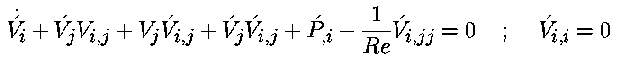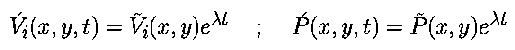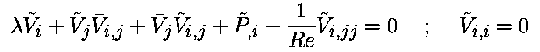Mathematical background
The stability analysis considers disturbance as the small deviation from the steady state. The unsteady solution of the Navier-Stokes equation is expressed as the sum of the steady solution and the disturbance:
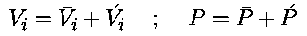
In resulting disturbance equation
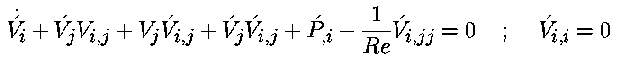
the space and time dependence is separated:
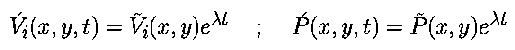
The partial differential eigenvalue problem
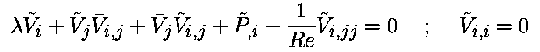
is linearised and discretized with penalty FEM:
It is a generalized eigenvalue problem:
Webmaster
Last modified: Wed Dec 15 11:25:30 CET 1999