 |
(6.49) |
Da der hier vorgestellte Formelapparat wenig anschaulich ist, soll im folgenden die Vorgehensweise noch einmal von einer anderen Seite betrachtet und damit einsichtiger dargestellt werden: Bei inkompressiblen Strömungen erfüllt der Druck die Funktion einer zusätzlichen Zwangsbedingung, die die Kontinuität des aus den Impulsgleichungen bestimmten Geschwindigkeitsfeldes sicherstellen muß. Die absolute Größe des Drucks ist dabei gleichgültig, weil in den Gleichungen nur Druckgradienten auftreten. Eine Glättung zur Vermeidung von Oszillationen des Drucks ist deshalb zulässig.
Betrachten wir zur Veranschaulichung eine Poissongleichung für den Druck, wie sie sich durch Ableitung der Impulsgleichungen herleiten läßt:
 |
(6.49) |
![]() steht dabei für Konvektions- und Diffusionsterm der
Impulsgleichung.
steht dabei für Konvektions- und Diffusionsterm der
Impulsgleichung.
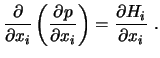 |
(6.50) |
Die Finite-Differenzen Approximation für die zweidimensionale Form dieser Gleichung liefert:
Zur Approximation der Druckgradienten gibt es zwei naheliegende Ansätze:
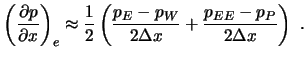 |
(6.52) |
Dies ist einer Approximation von gleicher Ordnung, wie sie in der
Impulsgleichug verwendet wird.
Das Einsetzen in Gleichung (6.51) ergibt:
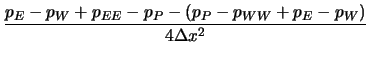 |
|||
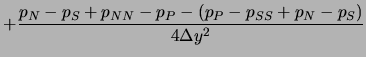 |
|||
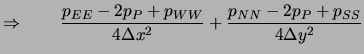 |
(6.53) |
Diese Gleichung ist zwar von hoher Genauigkeit, weist aber das typische Entkopplungsproblem auf (nur Druckwerte an jeweils versetzten Kontrollvolumen tauchen auf).
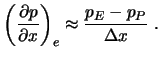 |
(6.54) |
Wird diese Gleichung für die Approximation benutzt, ergibt sich:
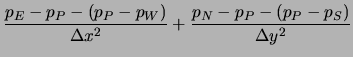 |
|||
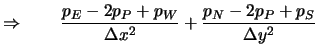 |
(6.55) |
Dieser Ansatz ist zwar aufgrund der schwächeren Approximation des Druckgradienten von geringerer Ordnung, vermeidet aber das Problem der Entkopplung von Druck und Geschwindigkeit.
Betrachten wir nun den Unterschied zwischen beiden Ansätzen in der
resultierenden Differenzengleichung:
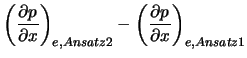 |
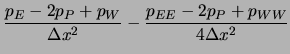 |
||
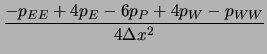 |
(6.56) | ||
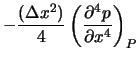 |
(6.57) |
Die erforderliche Korrektur der Approximation, um von einer
entkoppelten Form ausreichender Ordnung zu einer gekoppelten zu
gelangen, entspricht somit genau einer Glättung, die proportional
zur 4. Ableitung des Drucks ist. In einer solchen Formel
treten bei oszillierenden Druckwerten große Korrekturen auf,
während sie bei glattem Druckverlauf gegen null geht.
Ein gleichartiger Ansatz verbirgt sich auch hinter dem in den
Gleichungen (6.41) bis (6.45) beschriebenen
Korrekturmechanismus für die Geschwindigkeiten auf den
Kontrollvolumengrenzen.