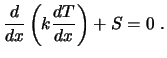 |
(3.5) |
Beobachten wir die KV-Formulierung an einem einfachen Beispiel. Die eindimensionale stationäre Wärmeleitung (vergleiche Kapitel 4.1) lautet:
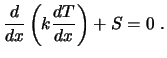 |
(3.5) |
Die Benennung benachbarter Punkte eines KV erfolgt nach der sog. Kompaßnotation:
Zur Vereinfachung verwenden wir eine Einheitsdicke in ![]() - und
- und
![]() -Richtung:
-Richtung:
![]() ,
,
![]() .
.
![$\displaystyle \int\limits_{w}^{e} \left[ {d \over dx} \left( k {dT \over dx} \right) + S \right] dx = 0 \ ,$](img188.png) |
(3.6) |
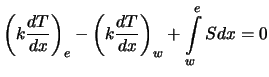 |
(3.7) |
An dieser Stelle muß eine Formel zur Beschreibung des
Ein Stufenprofil ist nicht sinnvoll, da
![]() an den
Kontrollvolumen-Wänden nicht definiert ist.
(siehe Abbildung 7)
an den
Kontrollvolumen-Wänden nicht definiert ist.
(siehe Abbildung 7)
Der Gradient ist an den Kontrollvolumen-Wänden kontinuierlich aber nicht definiert an den Gitterpunkten. Eine Berechnung dort ist aber auch nicht nötig. (siehe Abbildung 8)
führt auf:
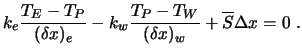 |
(3.10) |
Allgemeine Form:
mit
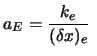 |
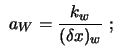 |
||
| (3.12) | |||
Die hier abgeleitete Form der Diskretisierungsgleichung kann als Satz von Koeffizienten für ein lineares Gleichungssystem (LGS) verstanden werden, das sich numerisch lösen läßt.