2D-Adaption

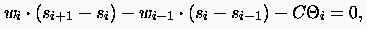
Man könnte nun alle Zeilen und/oder Spalten eines Rechengebietes mit der oben beschriebenen Methode durchlaufen. Diese Methode ist sicher nicht sehr sinnvoll, da sie im allgemeinen ein stark verzerrtes Gitter erzeugt. Bei Verwendung des 1D-Verfahrens auf jede Zeile/Spalte eines Gitters werden nur Informationen der aktuellen Linie verarbeitet, also kann sich jede Linie ohne Rücksicht auf Orthogonalität etc. frei einstellen. Somit wäre ein glattes Gitter purer Zufall. Da die meisten Lösungsverfahren auf glatten und möglichst orthogonalen Gittern wesentlich besser konvergieren als auf verzerrten, ist es nicht einsichtig, ein glattes Startgitter durch die Adaption, die ja eine Verbesserung der Lösung bezwecken soll, verzerren zu lassen. Im folgenden wird ein Verfahren - wiederum auf einer Federmodellanalogie basierend - vorgestellt, das eine glatte und orthogonale Punkteverteilung ermöglicht.

Betrachten wir eine Strömung auf einer leicht gekrümmten Fläche, z. B. auf der Oberseite eines Tragflügelprofils, die krummlinigen Koordinaten heißen $$ und $$.

Die Vorgehensweise ist nun wie folgt:

Auf der Linie j = 1 wird, wie oben beschrieben, die Punkteverteilung ausgerechnet (Die Linie j = 1 wird auf eine gerade Linie der Länge S transformiert, man führt die 1D-Adaption durch und transformiert die neue Punkteverteilung wieder auf die Flügeloberfläche zurück).

Auf den Linien j = 2,..,NJ wird nun eine zusätzliche Bedingung eingebaut: Am Punkt (i, j-1), das ist Punkt 'D' in der Skizze, wird eine Torsionsfeder angebracht. Diese Feder ist entspannt, wenn sich der betrachtete Punkt auf der Linie j = const. (Punkt A in der Skizze) auf Punkt A' befindet. Die Lage von A' ergibt sich aus einer 'Mittelung' zwischen der Geraden durch E und D sowie der Strecke $DA$_n, wobei $DA$_n die Normale auf die Strecke $DF$ darstellt (für j = 2 nimmt man nur die Normale, da es die Gerade durch E und D nicht gibt). Man kann nun für eine Linie j = const. das Kräftegleichgewicht anschreiben:

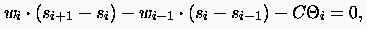(6.153)

mit $w$_i wie bei j = 1, allerdings wird $f$ aus dem gesamten Feld berechnet. $$_i ist der Winkel, um den die Torsionsfeder ausgelenkt wurde, und $C$ ist die Torsionsfederkonstante:

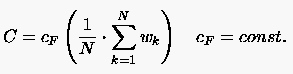(6.154)

Die Wirkung der Torsionsfeder läßt sich auch durch eine Zugfeder beschreiben, damit (6.153) als einzige Unbekannte $s$ enthält. Damit ergibt sich (6.153), geordnet nach $s$_i, zu

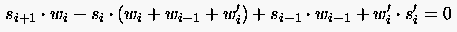(6.155)

mit 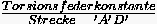als entsprechender Federkonstanten w'. Das Gleichungssystem (6.155) läßt sich mit dem TDMA lösen.

Die gesamte Prozedur läßt sich folgendermaßen zusammenfassen:

1. Auswahl einer geeigneten Sensorfunktion
2. Bestimmung zulässiger Minimal- und Maximalabstände
3. Transformation der krummlinigen Koordinaten auf eine Strecke
4. iterative Bestimmung von B
5. Berechnung der $w$_i
6. Berechnung der neuen Punkteverteilung
7. Rücktransformation Gerade $$ krummlinige Koordinaten

Die Schritte 3 bis 7 werden für alle $j$< 2 < NJ durchgeführt.