



Nächste Seite: Randbedingungen für die Druckkorrekturgleichung
Aufwärts: Der SIMPLE-Algorithmus
Vorherige Seite: Reihenfolge der Operationen des
Inhalt
In Kapitel 6.5 wurde der Term
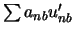 vernachlässigt auf dem Weg
zur Geschwindigkeitskorrekturformel (6.19).
vernachlässigt auf dem Weg
zur Geschwindigkeitskorrekturformel (6.19).
- Berücksichtigung des Terms würde alle Nachbarpunkte
involvieren, und voll implizite Lösung wäre notwendig. Vernachlässigung
führt auf die gleiche Form wie die allgemeine
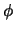 -Gleichung und macht das
Verfahren nicht mehr voll-, sondern nur noch partiell implizit
(semi-implizit).
-Gleichung und macht das
Verfahren nicht mehr voll-, sondern nur noch partiell implizit
(semi-implizit).
- Die Vernachlässigung verursacht keinen Fehler in der
konvergierten Lösung, da das ´´gesternte´´ Geschwindigkeitsfeld
bereits die
Kontinuität erfüllt. Die Herleitung der
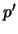 -Gleichung spielt dann keine
Rolle mehr.
-Gleichung spielt dann keine
Rolle mehr.
- Die Massenquelle
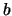 ist ein guter Konvergenzindikator.
ist ein guter Konvergenzindikator.
- Die Druckkorrektur ist lediglich ein vorübergehender Algorithmus,
der das konvergierte
Druckfeld nicht beeinflußt. Die Formulierung
beeinflußt aber die Konvergenzgeschwindigkeit.
- Die Druckkorrekturgleichung (Kapitel 6.6)
ist divergenzempfindlich, wenn
nicht unterrelaxiert wird. Unterrelaxation von
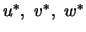 bei Lösungen
der Impulsgleichung bezogen auf vorangegangene Iterationswerte
bei Lösungen
der Impulsgleichung bezogen auf vorangegangene Iterationswerte 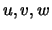 mit
mit
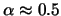 (Gleichung 4.51). Außerdem addieren wir nur
einen Bruchteil von
(Gleichung 4.51). Außerdem addieren wir nur
einen Bruchteil von 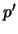 zu
zu 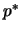 :
:
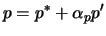 |
(6.27) |
mit
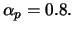
- In der nächsten Iteration wird
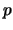 zu
zu 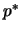 .
(
.
(
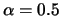 und
und
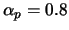 sind gute Anhaltswerte). Unterrelaxation
ist notwendig, da durch Fortlassen von
sind gute Anhaltswerte). Unterrelaxation
ist notwendig, da durch Fortlassen von
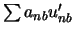 die Druckkorrektur
zu groß berechnet wird.
die Druckkorrektur
zu groß berechnet wird.
- In jeder Iteration erfüllen die korrigierten Geschwindigkeiten die
Kontinuitätsgleichung, was sich vorteilhaft auswirkt. Die
Geschwindigkeitskorrektur sollte nicht unterrelaxiert
werden.
- Kompressible Strömungen erfordern die kompressible Form der
Druckkorrekturgleichung (Kapitel 6.9).




Nächste Seite: Randbedingungen für die Druckkorrekturgleichung
Aufwärts: Der SIMPLE-Algorithmus
Vorherige Seite: Reihenfolge der Operationen des
Inhalt
Ulf Bunge
2003-10-10
![]() vernachlässigt auf dem Weg
zur Geschwindigkeitskorrekturformel (6.19).
vernachlässigt auf dem Weg
zur Geschwindigkeitskorrekturformel (6.19).