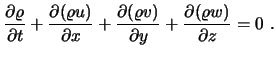 |
(6.22) |
Aus der Kontinuitätsgleichung leiten wir eine Gleichung für die Druckkorrektur ab. Wir nehmen an, daß die Dichte nicht direkt vom Druck abhängt (Diskussion später). Für einen dreidimensionalen Fall ist die Kontinuitätsgleichung
Integration über das Kontrollvolumen im Abbildung 47 (entspricht dem
Haupt-Kontrollvolumen für allgemeine Variable ![]() ).
).
Für die Integration von
![]() sei die
Dichte konstant im Kontrollvolumen. Geschwindigkeiten wie
sei die
Dichte konstant im Kontrollvolumen. Geschwindigkeiten wie ![]() an einer
Kontrollvolumen-Wand beschreiben den Massenfluß für die gesamte Wand.
Voll implizite Zeitdiskretisierung führt schließlich auf die
integrierte Form von (6.22)
an einer
Kontrollvolumen-Wand beschreiben den Massenfluß für die gesamte Wand.
Voll implizite Zeitdiskretisierung führt schließlich auf die
integrierte Form von (6.22)
Ersetzen der Geschwindigkeiten durch die Geschwindigkeitskorrekturformel
(6.19) - (6.21) ergibt die Diskretisierungsgleichung für ![]()
mit
![$\displaystyle b =
{(\varrho_P - \varrho_P^0) \Delta x \Delta y \Delta z \over \Delta t}
+ [(\varrho u^*)_w - (\varrho u^*)_e] \Delta y \Delta z$](img816.png) |
|||
| (6.26) |
Die Dichte liegt normalerweise nur an den Gitterpunkten vor, so daß die
Wand-Dichten wie ![]() geeignet interpoliert werden müssen.
Dabei muß der Wert von
geeignet interpoliert werden müssen.
Dabei muß der Wert von ![]() konsistent für die
beiden Kontrollvolumen berechnet werden, zu denen die Wand gehört
(Grundregel 1).
konsistent für die
beiden Kontrollvolumen berechnet werden, zu denen die Wand gehört
(Grundregel 1).
Aus (6.25) ist ersichtlich, daß der Term ![]() in der
Druckkorrekturgleichung im wesentlichen die linke Seite der
diskretisierten Kontinuitätsgleichung (6.23) darstellt,
ausgewertet für die gesternten Geschwindigkeiten.
in der
Druckkorrekturgleichung im wesentlichen die linke Seite der
diskretisierten Kontinuitätsgleichung (6.23) darstellt,
ausgewertet für die gesternten Geschwindigkeiten. ![]() bedeutet,
daß die gesternten Geschwindigkeiten die Kontinuitätsgleichung
erfüllen und keine Druckkorrektur notwendig ist. Der Term
bedeutet,
daß die gesternten Geschwindigkeiten die Kontinuitätsgleichung
erfüllen und keine Druckkorrektur notwendig ist. Der Term ![]() stellt
daher eine ´´Massenquelle´´ dar, die die Druckkorrekturen (vermittels
ihrer abgeleiteten Geschwindigkeitskorrekturen) auslöschen müssen.
stellt
daher eine ´´Massenquelle´´ dar, die die Druckkorrekturen (vermittels
ihrer abgeleiteten Geschwindigkeitskorrekturen) auslöschen müssen.
Mit der Formulierung aller notwendigen Gleichungen für die Berechnung der Geschwindigkeitskomponenten und des Drucks können wir das Gesamtverfahren darstellen.