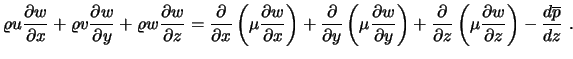Wärmeleitungsähnliche Probleme

Mit der bisher entwickelten Methode können nicht nur Wärmeleitungsprobleme gelöst werden, sondern auch

• Massendiffusion
  
• Elektromagnetische Felder
  
• Spezielle Strömungsprobleme, wie
  
  • Potentialströmung
    
  • Strömung in porösen Medien
    
  • Vollausgebildete Kanalströmung

Z.B. Impulsgleichung in z-Richtung, stationär

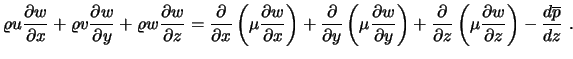$$\varrho u {\partial w \over \partial x} + \varrho v {\partial w \... ...left( \mu {\partial w \over \partial z} \right) - {d \overline{p} \over dz} \ .$$ (4.56)

Einfache $(u = v = 0)$ voll ausgebildete $(\partial w / \partial z = 0)$ Strömungen führen auf:

$$0 = {\partial \over \partial x} \left( \mu {\partial w \over \par... ...left( \mu {\partial w \over \partial y} \right) - {d \overline{p} \over dz} \ .$$ (4.57)

(4.57) ist eine Gleichung vom Wärmeleitungstyp, wenn $\phi = w,\ \Gamma = \mu ,\ S = - {d \overline{p} \over dz}$ gesetzt wird.

Z.B. Voll ausgebildeter Wärmeübergang

Energiegleichung für kleine Mach-Zahlen, stationär, ohne Dissipation:

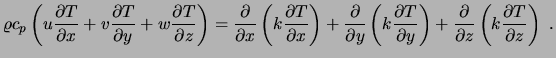$$\varrho c_p \left( u {\partial T \over \partial x} + v {\partial ... ...+ {\partial \over \partial z} \left( k {\partial T \over \partial z} \right)\ .$$ (4.58)

Unter den Annahmen $c_p = const$, Vernachlässigung der axialen Wärmeleitung, einfache Strömungen $(u = v = 0)$, voll ausgebildete axiale Strömung erhält man:

$$\varrho c_p w {\partial T \over \partial z} = {\partial \over \pa... ... {\partial \over \partial y} \left( k {\partial T \over \partial y} \right) \ .$$ (4.59)

Gleichung (4.59) ist vom Wärmeleitungstyp, wenn man setzt:

$$\phi = T, \quad \Gamma = k, \quad S = - \varrho c_p w {\partial T \over \partial z} \ .$$

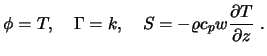Man kann daher einfache vollausgebildete Strömungen mit vollausgebildetem Wärmeübergang wie ein Wärmeleitungsproblem behandeln, wenn man die axiale Strömung formal als Quellterm in der Energiegleichung behandelt. Der Gradient $\partial T / \partial z$ muß bekannt oder berechenbar sein (möglich für bestimmte in z-Richtung ähnliche Temperaturprofile). Außerdem muß die $w$-Verteilung bekannt sein, z.B. als Lösung des voll ausgebildeten Strömungsproblems (4.57).