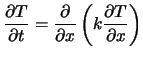Die allgemeine Diskretisierungsgleichung

Zunächst konzentrieren wir uns auf den instationären Term und lassen den Quellterm weg:

$${\partial T \over \partial t} = {\partial \over \partial x} \left( k {\partial T \over \partial x} \right)$$ (4.27)

mit $\varrho c = const.$ als Vorraussetzung, im Diffusionskoeffizient mit 'verarbeitet'.

Die Zeit ist eine einseitig gerichtete Koordinate, also ist ein Fortschreitungsverfahren in Zeitrichtung möglich: Wir berechnen die Lösung ausgehend von der Anfangsverteilung der Temperatur.
In einem typischen Zeitschritt: bei gegebenen Werten von $T$ zur Zeit $t$ sind $T$-Werte zur Zeit $t+\Delta t$ zu berechnen.
Es seien die alten Werte $T_P^0,\ T_E^0,\ T_W^0$ und die zur Zeit $(t + \Delta t)$ sind $T_P^1,\ T_E^1,\ T_W^1$. Diskretisierungsgleichung aus Integration von (4.27) über ein Kontrollvolumen (z.B. Abbildung 10) und über ein Zeitintervall von $t$ bis $t+\Delta t$ ist:

$$\int_w^e \int_t^{t+ \Delta t} {\partial T \over \partial t} dt dx... ...rtial \over \partial x} \left( k {\partial T \over \partial x} \right) dx dt\ .$$ (4.28)

Als Profilannahme für die Zeitableitung verwenden wir: der Wert von $T$ gilt im ganzen Kontrollvolumen, d.h. $T(x) = const$:

$$\int_w^e \int_t^{t+ \Delta t} {\partial T \over \partial t} dt dx = \Delta x (T_P^1 - T_P^0)\ .$$ (4.29)

In Analogie zur stationären Wärmeleitung für $k {\partial T \over \partial x}$ setzen wir:

$$\Delta x (T_P^1-T_P^0) = \int_t^{t + \Delta t} \left[ {k_e (T_E - T_P) \over (\delta x)_e} - {k_w (T_P - T_W) \over (\delta x )_w} \right] dt\ .$$ (4.30)

Nun ist die Profilannahme für die zeitliche Veränderung von $T_P,\ T_E,\ T_W$ von $t$ bis $t+\Delta t$ gesucht.
Allgemeine Darstellung einiger Möglichkeiten für $T(t)={\it linear}$:

$$\int_t^{t+ \Delta t} T_P dt = [f T_P^1 + (1 -f) T_P^0] \Delta t$$ (4.31)

mit Wichtungsfaktor $0 \le f \le 1$. Analoges gilt für die $T_E$- und $T_W$-Integrale.
Man erhält:

$${\Delta x \over \Delta t} (T_P^1 - T_P^0) = f \left[ {k_e (T_E^1 - T_P^1) \over (\delta x)_e} - {k_w (T_P^1 -T_W^1) \over (\delta x)_w} \right]$$ (4.32)

$$+ (1 - f) \left[ {k_e (T_E^0 -T_P^0) \over (\delta x)_e} - {k_w (T_P^0 -T_W^0) \over (\delta x)_w} \right] \ .$$

Im folgenden wird der Index 1 weggelassen, d.h. $T_P,\ T_W,\ T_E$ sind Werte zur Zeit $t+\Delta t$. Die Diskretisierungsgleichung lautet dann

$$a_P T_P = a_E [f T_E + (1-f) T_E^0] + a_W[f T_W + (1-f) T_W^0]$$ (4.33)

$$+ [a_P^0 - (1-f) a_E - (1-f) a_W] T_P^0$$

mit den Varianten Explizit, Crank-Nicolson und Voll Implizit:

$$f = \left\{ \begin{array}{ll} 0 & : \mbox{explizit} \\ 0.5 & : \mbox{Crank--Nicolson} \\ 1 & : \mbox{voll implizit} \end{array} \right.$$ (4.34)

Abbildung: Veranschaulichung der Werte von $f$ anhand der $T$-$t$-Verläufe

Wir bevorzugen die voll implizite Variante.

Explizit $(f=0)$ ergibt für (4.33):

$$a_P T_P = a_E T_E^0 + a_W T_W^0 + (a_P^0 - a_E - a_W) T_P^0 \ .$$ (4.35)

Vor dem Hintergrund der 2. Grundregel ist zu beachten, daß der Koeffizient von $T_P^0$ in (4.35) negativ werden kann.

Für $k = const$ und $\Delta x = (\delta x)_e = (\delta x)_w$ muß gelten

$$\Delta t < {(\Delta x)^2 \over 2 k}\ ,$$ (4.36)

sonst können physikalisch unsinnige Ergebnisse entstehen. (4.36) ist ein bekanntes Stabilitätskriterium für das explizite Schema. Wir haben es hier abgeleitet aus physikalischen Überlegungen auf der Basis der vier Grundregeln.

Crank-Nicolson ist bedingungslos stabil. Das bedeutet keineswegs, daß sich physikalisch realistische Ergebnisse für beliebige Zeit- und Ortsschrittweiten ergeben! Oft ergeben sich oszillierende Lösungen.

$\rightarrow$

Ein augenscheinlich vernünftiges lineares Profil ist gut nur für kleine Zeitintervalle. Für größere Zeitschritte tendiert die im wesentlichen exponentielle Abnahme zu einem steilen Abfall am Anfang mit einem flachen Auslauf.

Das voll implizite Schema ist realitätsnäher als das Crank-Nicolson-Schema, besonders für große $\Delta t$.

Die Forderung nach stets positivem Koeffizienten von $T_p^0$ in (4.33) erzwingt $f=1$. Ein voll implizites Schema ergibt immer ein physikalisch sinnvolles Verhalten.

Beachte: für kleine $\Delta t$ ist Crank-Nicolson genauer.