



Nächste Seite: Randbedingungen
Aufwärts: Wärmeleitung
Vorherige Seite: Nichtlinearität
Inhalt
Quellterm-Linearisierung
Wenn 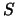 von
von 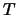 abhängt, schreiben wir den Quellterm
abhängt, schreiben wir den Quellterm
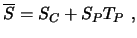 |
(4.14) |
denn erstens erlaubt unser nominell lineares Rahmenwerk nur formal
lineare Abhängigkeit, und zweitens ist die Berücksichtigung linearer
Abhängigkeit besser als die Annahme 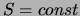 . Falls
. Falls 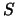 eine
nichtlineare Funktion von
eine
nichtlineare Funktion von 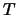 ist, müssen wir linearisieren,
d.h.
ist, müssen wir linearisieren,
d.h. 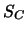 und
und 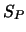 angeben, die ihrerseits wieder von
angeben, die ihrerseits wieder von 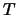 abhängen
können:
abhängen
können:
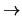 dies erfordert iterative Neuberechnung. Die
Linearisierung sollte die
dies erfordert iterative Neuberechnung. Die
Linearisierung sollte die 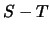 -Beziehung gut repräsentieren.
Außerdem muß die Grundregel über nichtpositives
-Beziehung gut repräsentieren.
Außerdem muß die Grundregel über nichtpositives 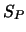 beachtet
werden (Regel 3). Prinzipiell sind viele Arten der Aufspaltung von
beachtet
werden (Regel 3). Prinzipiell sind viele Arten der Aufspaltung von
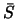 in
in 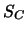 und
und 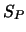 denkbar.
denkbar.
Beispiele:
- 1.
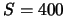
- dann
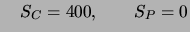
- 2.
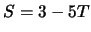
- dann
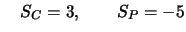
- 3.
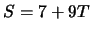
- dann
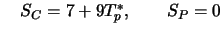
-
- nicht empfehlenswert:
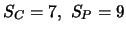
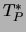 ist der Startwert oder der Wert aus der vorangegangenen Iteration.
ist der Startwert oder der Wert aus der vorangegangenen Iteration.
- 4.
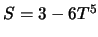
- verschiedene Möglichkeiten:
- 4.1
-
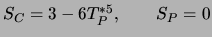
''lazy-person approach'' für komplizierte Quellterme.
- 4.2
-
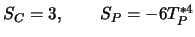
nicht falsch, aber nicht die beste Darstellung von 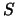
- 4.3
- Empfehlung: Ausdrücken von
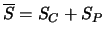
durch die Tangente (Taylorreihen-Entwicklung):
-
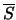
-
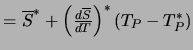 ;
;
hier:
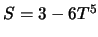 :
:
-
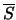
-
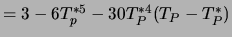
-
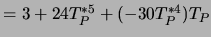
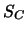
-

- 4.4
- Auch möglich:
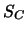
-
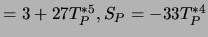
-
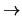
- alle Möglichkeiten sind prinzipiell zulässig, da
alle bei Konvergenz denselben Quellterm darstellen. Sie beeinflussen
aber das Konvergenzverhalten (Abbildung 14).
Abbildung 14:
Quelltermlinearisierung und Konvergenzverhalten
|
|
4.3 ergibt optimale Konvergenz; 4.1, 4.2 können
divergieren; 4.4 konvergiert sehr langsam.




Nächste Seite: Randbedingungen
Aufwärts: Wärmeleitung
Vorherige Seite: Nichtlinearität
Inhalt
Ulf Bunge
2003-10-10
![]() von
von ![]() abhängt, schreiben wir den Quellterm
abhängt, schreiben wir den Quellterm
![]() . Falls
. Falls ![]() eine
nichtlineare Funktion von
eine
nichtlineare Funktion von ![]() ist, müssen wir linearisieren,
d.h.
ist, müssen wir linearisieren,
d.h. ![]() und
und ![]() angeben, die ihrerseits wieder von
angeben, die ihrerseits wieder von ![]() abhängen
können:
abhängen
können:
![]() dies erfordert iterative Neuberechnung. Die
Linearisierung sollte die
dies erfordert iterative Neuberechnung. Die
Linearisierung sollte die ![]() -Beziehung gut repräsentieren.
Außerdem muß die Grundregel über nichtpositives
-Beziehung gut repräsentieren.
Außerdem muß die Grundregel über nichtpositives ![]() beachtet
werden (Regel 3). Prinzipiell sind viele Arten der Aufspaltung von
beachtet
werden (Regel 3). Prinzipiell sind viele Arten der Aufspaltung von
![]() in
in ![]() und
und ![]() denkbar.
denkbar.
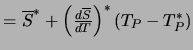 ;
;