Randbedingungen

Für jeden inneren Punkt haben wir eine Diskretisierungsgleichung für die Temperatur an diesem Punkt aus der Gleichung für das entsprechende Kontrollvolumen (siehe Abbildung 15).

Abbildung 15: Innere Kontrollvolumen

Wenn Randtemperaturen gegeben sind, werden keine zusätzlichen Gleichungen benötigt.

Typische Randbedingungen sind:

1.

Randtemperatur $T_B$ gegeben.

2.

Randwärmefluß $q_B$ gegeben.

3.

Randwärmefluß als eine (lineare) Funktion von $T_B$ gegeben.

Für 2. und 3. muß eine zusätzliche Gleichung konstruiert werden (Beispiel linker Rand, Abbildung 16):

Abbildung 16: Linker Rand

Integration der Differentialgleichung über das ''halbe'' Kontrollvolumen am Rand ergibt die
Halb-Kontrollvolumen-Gleichung:

$$q_B - q_i + (S_C + S_P T_B) \Delta x = 0\ .$$ (4.15)

(Beachte: $q=-k {dT \over dx})$. Der Wärmefluß $q_i$ kann geschrieben werden als

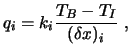$$q_i = k_i {T_B - T_I \over (\delta x)_i}\ ,$$ (4.16)

womit sich ergibt:

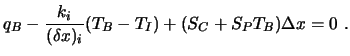$$\smallskip q_B - {k_i \over (\delta x)_i} (T_B - T_I) + (S_C + S_P T_B) \Delta x = 0\ .$$ (4.17)

Das weitere Vorgehen hängt davon ab, wie der Randwärmefluß $q_B$ gegeben ist. Falls $\underline{q_B \ \mbox{selbst}}$ gegeben ist, ergibt sich die Diskretisierungsgleichung zu:

$$a_B T_B = a_I T_I + b\ ,$$ (4.18)

mit

$$a_I = {k_i \over (\delta x)_i} \ ; b = S_C \Delta x + q_B \ ;$$ (4.19)

$$a_B = a_I - S_P \Delta x \ .$$

Falls $\underline{q_B \ \mbox{als lineare Funktion}}$ der Randtemperatur $T_B$ gegeben ist:

$$q_B = f_C + f_P T_B \ ,$$ (4.20)

wie z.B. bei konvektivem Wärmeübergang: $q_B = h(T_{\infty} - T_B)$, dann erhalten wir für (4.18) die Koeffizienten

$$a_I = {k_i \over (\delta x)_i} \ ; b = S_C \Delta x + f_C$$ (4.21)

$$a_B = a_I - S_P \Delta x - f_P \ .$$

Für den linearen Wärmefluß fordern wir genau wie für den linearisierten Quellterm, daß $f_P \le 0$ ist, damit $f_P$ einen positiven Beitrag zum (Diagonalenelement-) Koeffizienten $a_B$ liefert.

Falls $\underline{q_B \ \mbox{eine nichtlineare Funktion}}$ von $T_B$ ist, linearisieren wir $q_B$ nach den gleichen Regeln wie für den Quellterm (Taylorreihen-Entwicklung):

$$q_B = q_B^* + \left( {dq_B \over dT_B} \right)^* (T_B - T_B^*) \ ;$$ (4.22)

womit wir für (4.20) erhalten:

$$f_C = q_B^* - \left( {dq_B \over dT_B} \right)^* T_B^* \ ,$$ (4.23)

$$f_P = \left( {dq_B \over dT_B} \right)^* \ .$$

Beispiel: Konvektiver und Strahlungs-Wärmeübergang:

$$q_B = 5 (T_{\infty} - T_B) + 2(T_{\infty}^4 - T_B^4)$$ (4.24)

ergibt

$$f_C = 5 T_{\infty} + 2T_{\infty}^4 + 6 T_B^{*4} , \qquad f_P = -(5 + 8 T_B^{*3})$$ (4.25)