



Nächste Seite: Wärmeleitung
Aufwärts: Diskretisierungskonzept der Finite-Volumen-Methode
Vorherige Seite: Quelltermbehandlung
Inhalt
Zur Sicherung von physikalisch realistischen Ergebnissen und
globaler Erhaltung lassen sich vier wesentliche Grundforderungen
formulieren:
- Regel 1:
- Konsistenz an den Kontrollvolumen-Wänden.
An einer Wand, die zu zwei benachbarten Kontrollvolumen gehört,
muß der
Fluß durch diese Wand durch den gleichen Ausdruck in den
Diskretisierungsgleichungen für die beiden Kontrollvolumen dargestellt
werden.
Der Wärmefluß, der ein Kontrollvolumen verläßt, muß
identisch sein mit dem Fluß, der in das nächste Kontrollvolumen durch
die gleiche Wand eintritt. Sonst ist keine Erhaltung möglich.
 Wandflüsse erfordern eigenständige
Betrachtung.
Wandflüsse erfordern eigenständige
Betrachtung.
- Regel 2:
- Positive Koeffizienten.
Alle Koeffizienten
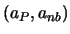 müssen immer positiv sein. Die
Koeffizientendefinition (3.16) erfüllt Regel 2. Eine
Verletzung der Regel führt i.a. auf physikalisch unrealistische
Ergebnisse.
müssen immer positiv sein. Die
Koeffizientendefinition (3.16) erfüllt Regel 2. Eine
Verletzung der Regel führt i.a. auf physikalisch unrealistische
Ergebnisse.
- Regel 3:
- Quellterm-Linearisierung mit negativer Steigung.
Wird der Quellterm durch
linearisiert, muß stets
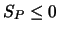 sein. Dadurch wird die
Diagonaldominanz der Matrix gesichert (verstärkt). Dies ist vor
allem bei der Verwendung von Punktverfahren zur Lösung des
Gleichungssystems wichtig.
sein. Dadurch wird die
Diagonaldominanz der Matrix gesichert (verstärkt). Dies ist vor
allem bei der Verwendung von Punktverfahren zur Lösung des
Gleichungssystems wichtig.
- Regel 4:
- Summe der Nachbarkoeffizienten
ohne Anteile aus (beliebig behandeltem) Quellterm.
Wir fordern
für Situationen, in denen die DGL weiter erfüllt bleibt, wenn man eine
Konstante zur abhängigen Variablen addiert. Die DGL enthält oft nur
Ableitungen der abhängigen Variablen 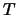 . Dann erfüllen sowohl
. Dann erfüllen sowohl 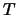 als
auch
als
auch
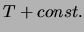 die DGL. Das muß durch die Diskretisierungsgleichung
wiedergegeben werden.
die DGL. Das muß durch die Diskretisierungsgleichung
wiedergegeben werden.
Die vier Grundregeln gelten für alle (bisherigen und weiteren) Schritte. Sie
sind anwendbar auf die allgemeine Variable 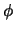 . Sie finden ihre Begründung
unter anderem in der Anwendung iterativer Lösungsverfahren (siehe Skript zu ``Numerische
Methoden der Thermo- und Fluiddynamik'' und Kapitel 8).
Der Konvektionsterm in der
allgemeinen DGL (2.13) erfordert spezielle Formulierungen
(
. Sie finden ihre Begründung
unter anderem in der Anwendung iterativer Lösungsverfahren (siehe Skript zu ``Numerische
Methoden der Thermo- und Fluiddynamik'' und Kapitel 8).
Der Konvektionsterm in der
allgemeinen DGL (2.13) erfordert spezielle Formulierungen
(
 Kapitel 5). Die anderen drei Terme werden im Rahmen der
Wärmeleitung (Kapitel 4) behandelt.
Kapitel 5). Die anderen drei Terme werden im Rahmen der
Wärmeleitung (Kapitel 4) behandelt.




Nächste Seite: Wärmeleitung
Aufwärts: Diskretisierungskonzept der Finite-Volumen-Methode
Vorherige Seite: Quelltermbehandlung
Inhalt
Ulf Bunge
2003-10-10
![]() sein. Dadurch wird die
Diagonaldominanz der Matrix gesichert (verstärkt). Dies ist vor
allem bei der Verwendung von Punktverfahren zur Lösung des
Gleichungssystems wichtig.
sein. Dadurch wird die
Diagonaldominanz der Matrix gesichert (verstärkt). Dies ist vor
allem bei der Verwendung von Punktverfahren zur Lösung des
Gleichungssystems wichtig.
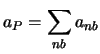
![]() . Dann erfüllen sowohl
. Dann erfüllen sowohl ![]() als
auch
als
auch
![]() die DGL. Das muß durch die Diskretisierungsgleichung
wiedergegeben werden.
die DGL. Das muß durch die Diskretisierungsgleichung
wiedergegeben werden.