



Nächste Seite: Quellterm und instationärer Term
Aufwärts: Krummlinige Koordinaten
Vorherige Seite: Konvektion
Inhalt
Größere Unterschiede zu der Behandlung in kartesischen Gittern
treten beim Diffusionsterm auf. Die Diskretisierung (z.B. am ''east''
Rand des Kontrollvolumens) in krummlinigen Koordinaten erfolgt analog
zur Vorgehensweise in (5.8) in leicht veränderter Form.
Der Diffusionsterm wird in einen impliziten und einen expliziten Anteil
aufgeteilt. Der implizite Anteil repräsentiert dabei am ''east''-Rand
den Fluß in 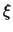 -Richtung, d.h. senkrecht zur
Kontrollvolumenoberfläche, während
der explizite Anteil den Fluß in
-Richtung, d.h. senkrecht zur
Kontrollvolumenoberfläche, während
der explizite Anteil den Fluß in 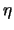 -Richtung wiedergibt:
-Richtung wiedergibt:
Impliziter Anteil
Expliziter Anteil
![$\displaystyle = -\frac{\Gamma_e}{J} (\phi_{ne}-\phi_{se}) \left[ (y_E - y_P)(y_{ne}-y_{se})+(x_E - x_P)(x_{ne}-x_{se}) \right] \ .$](img984.png) |
(7.14) |
Diese Aufteilung ist nötig, weil für die implizite Lösung in einem
Gleichungssystem mit vertretbarem Aufwand nur auf die Variablenwerte
an den Kontrollvolumenzentren zugegriffen werden kann, die als
Unbekannte zur Verfügung stehen, nicht aber auf Werte an den
Kontrollvolumenecken. Hier werden die interpolierten Werte der
letzten Iteration verwendet (explizite Behandlung). Der explizite
Anteil wird auch als Kreuzdiffusion bezeichnet.
Das Auftauchen der Kreuzdiffusion geschieht analog zum Auftreten
einer gemischten Ableitung
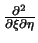 bei der
Approximation des Diffusionsterms mit Finiten-Differenzen
(siehe [33]).
bei der
Approximation des Diffusionsterms mit Finiten-Differenzen
(siehe [33]).
Bei der numerischen Lösung gehen die expliziten Anteile in den
Quellterm ein:
![$\displaystyle S_{\phi, Kreuzdiffusion} = - \frac{\Gamma_e}{J} (\phi_{ne}-\phi_{...
... \ \left[ (x_E - x_P) (x_{ne}-x_{se}) + (y_E - y_P) (y_{ne}-y_{se}) \right] \ .$](img986.png) |
(7.15) |
Da wir den Diffusionsfluß über eine Kontrollvolumenwand durch
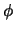 -Werte an zwei Gitterpunkten ausdrücken, ist es wichtig, daß
diese Wand senkrecht zur Verbindungslinie der beiden Gitterpunkte liegt.
Ist das Gitter überall orthogonal, d.h. stehen die
-Werte an zwei Gitterpunkten ausdrücken, ist es wichtig, daß
diese Wand senkrecht zur Verbindungslinie der beiden Gitterpunkte liegt.
Ist das Gitter überall orthogonal, d.h. stehen die
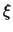 - und
- und 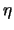 -Linien aufeinander senkrecht, so verschwinden die
Kreuzdiffusionsanteile
-Linien aufeinander senkrecht, so verschwinden die
Kreuzdiffusionsanteile
Kreuzdiffusion![$\displaystyle = \Gamma_e \ \Delta A_e \left[ \frac{\partial \eta}{\partial x_i} \frac{\partial \phi }{\partial \eta} \ n_i \right]_e \ ,$](img987.png) bzw. bzw.![$\displaystyle \qquad = \Gamma_n \ \Delta A_n \left[ \frac{\partial \xi}{\partial x_i} \frac{\partial \phi }{\partial \xi} \ n_i \right]_n \ .$](img988.png) |
(7.16) |
Bei Orthogonalität gilt:
und unter Verwendung von (7.10) und (7.8) für die
Kreuzdiffusion:
Aus der (lokalen) Orthogonalitätsbedingung
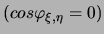 folgt somit direkt das Verschwinden
der Kreuzdiffusionsterme.
folgt somit direkt das Verschwinden
der Kreuzdiffusionsterme.
Die Aufteilung der Diffusion in einen expliziten und einen
impliziten Anteil verlangsamt im Vergleich zu einer komplett
impliziten Methode zwar die Konvergenz, im konvergierten Zustand ist
das Gleichungssystem jedoch genauso erfüllt.




Nächste Seite: Quellterm und instationärer Term
Aufwärts: Krummlinige Koordinaten
Vorherige Seite: Konvektion
Inhalt
Ulf Bunge
2003-10-10
![]() -Richtung, d.h. senkrecht zur
Kontrollvolumenoberfläche, während
der explizite Anteil den Fluß in
-Richtung, d.h. senkrecht zur
Kontrollvolumenoberfläche, während
der explizite Anteil den Fluß in ![]() -Richtung wiedergibt:
-Richtung wiedergibt:
![$\displaystyle \left[ \Gamma \ \Delta A \frac{\partial \xi^k}{\partial x_i}
\frac{\partial \phi }{\partial \xi^k} \ n_i \right]_e$](img977.png)
![$\displaystyle \Gamma_e \ \Delta A_e \left[ \frac{\partial \xi^k}{\partial x}
\f...
...artial \xi^k}{\partial y}
\frac{\partial \phi }{\partial \xi^k} \ n_y \right]_e$](img978.png)
![$\displaystyle \underbrace{
\Gamma_e \Delta A_e \left[
\frac{\partial \xi}{\part...
...artial y}
\frac{\partial \phi }{\partial \eta} \ n_y \right]_e }_{explizit} \ .$](img979.png)
![$\displaystyle \Gamma_e \ \Delta A_e \
\left[ \frac{\partial \phi}{\partial \xi...
...ac{\partial \phi}{\partial \xi}
\frac{\partial \xi}{\partial y} \ n_y \right]_e$](img980.png)
![$\displaystyle \frac{\Gamma_e}{J} (\phi_E - \phi_P) \left[ (y_{ne}-y_{se})^2
+ (x_{ne}-x_{se})^2 \right] \ .$](img982.png)
![$\displaystyle \Gamma_e \ \Delta A_e \ \left[ \frac{\partial \phi}{\partial \eta...
... A_e \ (\phi_{ne}-\phi_{se}) \left[ \eta_{,x} \ n_x + \eta_{,y} \ n_y \right]_e$](img983.png)
![$\displaystyle = -\frac{\Gamma_e}{J} (\phi_{ne}-\phi_{se}) \left[ (y_E - y_P)(y_{ne}-y_{se})+(x_E - x_P)(x_{ne}-x_{se}) \right] \ .$](img984.png)
![$\displaystyle S_{\phi, Kreuzdiffusion} = - \frac{\Gamma_e}{J} (\phi_{ne}-\phi_{...
... \ \left[ (x_E - x_P) (x_{ne}-x_{se}) + (y_E - y_P) (y_{ne}-y_{se}) \right] \ .$](img986.png)
![$\displaystyle = \Gamma_e \ \Delta A_e \left[ \frac{\partial \eta}{\partial x_i} \frac{\partial \phi }{\partial \eta} \ n_i \right]_e \ ,$](img987.png) bzw.
bzw.![$\displaystyle \qquad = \Gamma_n \ \Delta A_n \left[ \frac{\partial \xi}{\partial x_i} \frac{\partial \phi }{\partial \xi} \ n_i \right]_n \ .$](img988.png)
![$\displaystyle \Rightarrow \left[ \frac{\partial \eta}{\partial x} \ n_x
+\frac{\partial \eta}{\partial y} \ n_y \right]_e$](img993.png)
![$\displaystyle \Rightarrow \left[ \frac{\partial \xi}{\partial x} \ n_x
+\frac{\partial \xi}{\partial y} \ n_y \right]_n$](img994.png)