Koordinatensysteme

Betrachten wir ein allgemeines, krummliniges Koordinatensystem mit den Koordinatenlinien $\xi^k =(\xi^1, \xi^2, \xi^3 ) = (\xi, \eta, \zeta)$, das sich an den lokalen Gitterlinien ausrichtet. Im Zusammenhang mit der numerischen Behandlung der Bilanzgleichungen sind nun eine Reihe von Transformationen notwendig. Zum Verständnis der Transformationsbeziehungen soll zuerst auf die Eigenschaften des Koordinatensystems eingegangen werden.

Der Basisvektor

$$\underline{g}_k = \frac{\partial x_i}{\partial \xi^k} \underline{e}_i \ ,$$

weist an jedem Punkt des Raums in Richtung der Koordinatenlinie $\xi^k$. Üblicherweise definiert man krummlinige Koordinaten auf der Grundlage zweier komplementärer Basissysteme (i.Allg. holonome Basen):

$$\underline{g}^k = \frac{\partial \xi^k}{\partial x_i} \underline{e}_i \ ,$$

mit

$$\underline{e}_i=\frac{\partial \xi^k}{\partial x_i} \underline{g}_k =\frac{\partial x_i}{\partial \xi^k} \underline{g}^k \qquad \frac{\partial \xi^k}{\partial x_i} \frac{\partial x_i}{\partial \xi^j} = \delta_j^k = \delta_{kj} \ .$$ (7.3)

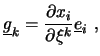
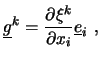
Der Transformationszusammenhang zwischen $x_i$ und $\xi^k$ wird durch mehrere unterschiedliche Metrikterme beschrieben. Von Bedeutung ist vor allem die Transformationsmatrix $\underline{\underline{J}}$ (Jakobi-Matrix) und die Funktionaldeterminante $J$ der Transformation des kartesischen Koordinatensystems in das lokale System des Rechengitters. $\underline{\underline{J}}$ bildet dabei die Matrix der kovarianten Metrikkoeffizienten:

$$J = det ( \underline{\underline{J}} ) \qquad \underline{\underline{J}} = \frac{\partial (x_1, x_2, x_3)... ...eta} & y_{,\zeta} \\ z_{,\xi} & z_{,\eta} & z_{,\zeta} \end{array} \right] \ ,$$ (7.4)

oder im zweidimensionalen Fall:

$$J = (\underline{\underline{J}}) = \left[ \begin{array}{cc} x_{,\xi} & x_{,\eta} \\ y_{,\xi} & y_{,\eta} \end{array} \right] = x_{,\xi} y_{,\eta} - x_{,\eta} y_{,\xi} \ .$$ (7.5)

Im folgenden soll die Herleitung wegen der besseren Übersichtlichkeit komplett auf zweidimensionale Fälle beschränkt bleiben. Mit (7.3) und Inversion ergeben sich die erforderlichen Transformationsbeziehungen für die Metrikterme:

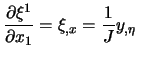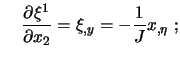$$\frac{\partial \xi^1}{\partial x_1} = \xi_{,x} = \frac1J y_{,\eta} \ ; \quad \frac{\partial \xi^1}{\partial x_2} = \xi_{,y} = -\frac1J x_{,\eta} \ ;$$ (7.6)

$$\frac{\partial \xi^2}{\partial x_2} = \eta_{,y} = \frac1J x_{,\xi} \ ; \quad \frac{\partial \xi^2}{\partial x_1} = \eta_{,x} = -\frac1J y_{,\xi} \ .$$

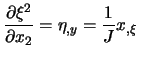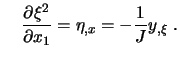Die Geometrie wird im Allgemeinen in Form der Koordinaten $x$ und $y$ der Kontrollvolumenzentren und der Gitterknotenpunkte bzw. Kontrollvolumenecken gespeichert (siehe Abbildung 53).

Abbildung: Benennung der Kontrollvolumenzentren, Grenzflächen und Eckpunkte

Üblicherweise wird der frei wählbare Skalierungsfaktor des natürlichen Koordinatensystems so gewählt, daß die Längen über ein Kontrollvolumen gerade ''1'' ergeben. Die Metrikterme können dann am ''east'' Rand über

$$x_{,\xi}=(x_E - x_P) \quad ; \quad y_{,\xi}=(y_E - y_P)$$ (7.7)

$$x_{,\eta}=(x_{ne}-x_{se}) \quad ; \quad y_{,\eta}=(y_{ne}-y_{se}) \ .$$

berechnet werden.

Ausgehend von einer beliebigen, zweidimensionalen Transportgleichung (5.38) soll nun die Diskretisierung in einem allgemeinen, krummlinigen Koordinatensystem abgeleitet werden. Die Integration der Differentialgleichung

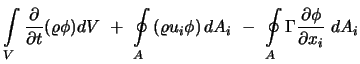$$\int \limits_V \frac{\partial}{\partial t} (\varrho \phi) dV \ + ... ...ht) dA_i \ - \ \oint \limits_A \Gamma \frac{\partial \phi}{\partial x_i} \ dA_i = \int \limits_V S dV \ ,$$ (7.8)

über ein Kontrollvolumen $V$ bzw. die Kontrollvolumenoberflächen $A$ führt dann im krummlinigen System auf

$$\left.\frac{\partial (\varrho \phi)}{\partial t} \Delta V \right\... ...lta A \ \phi \right]_w^e + \left[ \varrho u_i n_i \ \Delta A \ \phi \right]_s^n$$

$$- \left[ \Gamma \frac{\partial \xi^k}{\partial x_i} \frac{\partia... ...{\partial x_i} \frac{\partial \phi }{\partial \xi^k} \ n_i \Delta A \right]_s^n = S \ \Delta V \ ,$$

$$\left. \frac{(\varrho \phi)^1 -(\varrho \phi)^0}{\Delta t} \Delta V \right\vert _P + F_e \phi_e - F_w \phi_w + F_n \phi_n - F_s \phi_s$$

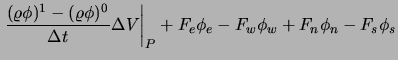$$- \Gamma_e \ \Delta A_e \left[ \frac{\partial \xi^k}{\partial x_i... ...tial \xi^k}{\partial x_i} \frac{\partial \phi }{\partial \xi^k} \ n_i \right]_w$$

$$- \Gamma_n \ \Delta A_n \left[ \frac{\partial \xi^k}{\partial x_i... ...tial \xi^k}{\partial x_i} \frac{\partial \phi }{\partial \xi^k} \ n_i \right]_s = S \ \Delta V \ .$$ (7.9)

Dabei sind $n_i$ die Komponenten des normierten Flächennormalenvektors einer Kontrollvolumenoberfläche und $\Delta A$ die Größe dieser Fläche. Wie aus Abbildung 53 zu entnehmen ist, ergibt sich der hierbei auftauchende Ausdruck $\Delta A_e \ \underline{n}_e$ bzw. die analog an den übrigen Kontrollvolumenseiten auftretenden Terme zu:

$$\Delta A_e \ \underline{n}_e = \left( \begin{array}{c} y_{,\eta} ... ...ne{n}_n = \left( \begin{array}{c} y_{,\xi} \\ - x_{,\xi} \end{array} \right)_n .$$ (7.10)