Unsteady flow structures in the wake

The numerical simulations presented here are based on the two-dimensional Reynolds-averaged approach. One result of the simulations is that unsteadiness occurs clearly only for low angles of attack. Here the flow structures are much more clearly evident than at higher incidence, where interaction with other separation processes is dominating. Therefore, first investigations are focused on a case with $\alpha=0^\circ$. Beside the mean quantities, the computational results also provide the unsteady behavior of the entire flow field and especially the structures of the flow behind the Gurney flap. Analysis of the time depending lift coefficient show that it can be characterized by one dominant frequency corresponding to the vortex shedding for all investigated cases. Table lists the Strouhal-number which represents the dominant shedding frequency normalized by the flap height. The fluctuation intensity based on the RMS value of the lift coefficient is defined by:

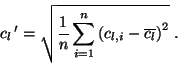$$c_l\,' =\sqrt{ \frac{1}{n} \sum_{i=1}^{n} \left( c_{l,i}-\overline{c_l} \right)^2} \ .$$ (3)

The characteristic behavior of the predicted frequencies is in good agreement with those measured by hot-wire anemometry [21]. For increasing flap heights the frequency decreases. At the same time however, the experimental Strouhal-number increases and assymptotically reaches $St \approx 0.18$ for very large Gurney-flaps ($h/c > 5\%$). Compared to the experiments [7,21] reporting $St=0.14$ for $h/c=1\%$ the Strouhal-number is slightly underestimated in the computations ($St=0.115$).

In the case of the clean airfoil and for the smallest Gurney-flap ($h/c=0.5\%$) almost no unsteadiness can be identified in the lift coefficient and $c_l\,'$ remains under $10^{-4}$. For large flap heights, the lift fluctuations become more eminent and grow superproportionally to the flap height in a similar manner to the extra drag induced by the Gurney-flap. This behavior is an indication that the intensity of vortex shedding characterized by $c_l\,'$ is responsible for the drag augmentation.

Table: Integral quantities and dominant frequency for $\alpha=0^\circ$ and varying flap height.

			$\overline{c_l}$		$c_l\,'$		$\overline{c_d}$		$St$
HQ17			$0.636$		$0.0000$		$0.0080$		$0.117$
$h/c=0.5\%$			$0.709$		$0.0003$		$0.0085$		$0.098$
$h/c=1.0\%$			$0.855$		$0.0044$		$0.0113$		$0.115$
$h/c=1.5\%$			$0.957$		$0.0144$		$0.0163$		$0.150$
$h/c=2.0\%$			$1.035$		$0.0167$		$0.0221$		$0.160$

The flow field is analyzed based on the vorticity in the $x$-$y$-plane (fig. ) where red marks clockwise rotating vortices and blue those rotating anti-clockwise. One single principle behavior can be observed for each flap height: Two shear layers appear that continuously separate from the top and the bottom end of the flap. After a short distance they start to roll up forming alternating vortices of counteracting direction of rotation. This phenomenon is called an absolute instability. As the mean flow field is directed slightly downwards ($\gamma>0$), near to the bottom end of the flap the lower vortices dominates. The vortex street is convected downstream until the mesh becomes too coarse to avoid its dissipation. Although the size of typical structures depends on the flap height, the relation is not proportional; the vortices grow slower. The shape of the occurring flow structures is comparable to PIV measurements for a Gurney-flap in ground effect by Zerihan and Zhang [21].

Figure: Snapshots of flow structures in the wake of Gurney-flaps with varying height (iso-contours of vorticity); upper line: $h/c=0.5\%$; center line: $h/c=1.5\%$; lower line: $h/c=2.0\%$.

A detailed description of the flow phenomena in the wake of Gurney-flaps requires the dependency of the flow structures on the angle of attack to be captured. In fig. the flow structures are plotted for varying angle of attack ( $0^\circ \le \alpha \le 4^\circ$) behind a Gurney-flap of $h/c=0.5\%$. These hardly differ in frequency, intensity or vortex size. In the case of further increased incidence however, the intensity of vortex shedding decreases and finally is no longer noticeable when the asymmetry between the boundary layer thicknesses on the suction and pressure sides causes the absolute instability to vanish. In this case, trailing edge separation on the suction side starts to occur which dominates the complete airfoil flow.

Figure: Snapshots of flow structures in the wake of Gurney-flaps with $h/c=0.5\%$ for varying angle of attack: upper line: $\alpha=0^\circ$; center line: $\alpha=2^\circ$; lower line: $\alpha=4^\circ$.