Lagrangesche und Eulersche Darstellung

Es gibt verschiedene Koordinaten und Betrachtungsweisen, die unterschiedliche mathematische Formulierungen erfordern. Nach [3] gibt es folgende vier Beschreibungen der Bewegung eines Kontinuums:

• Materielle Darstellung (Eng.: material description): Die unabhängigen Variablen sind das Teilchen $X$ und die Zeit $t$.
• Referenz-Darstellung (Eng.: referential description): Die unabhängigen Variablen sind der Ort $$X des Teilchens in einer beliebig gewählten Referenzkonfiguration und die Zeit $t$. In der Elastizitätstheorie wird meistens der unbelastete, spannungsfreie Zustand als Referenzkofiguration gewählt. Wird als Referenzkonfiguration die tatsächliche Anfangskonfiguration zum Zeitpunkt $t=0$ gesetzt, so spricht man von der Lagrangeschen Darstellung. Häufig wird dann bei anderen Autoren von der materiellen Darstellung gesprochen, wenn die Referenzposition $$X für das materielle Teilchen $X$ aus der ersten Darstellung verwendet wird.
• Räumliche Darstellung (Eng.: spatial description): Die unabhängigen Variablen sind die gegenwärtige Position $$x, die von dem Teilchen zur Zeit $t$ eingenommen wird, und die gegenwärtige Zeit $t$. Die Räumliche Darstellung bezieht sich also auf einen bestimmten Teil des Raumes anstatt auf einen bestimmten Teil der Materie. Diese in der Fluidmechanik am häufigsten verwendete Darstellung wird auch die Eulersche Darstellung genannt.
• Relative Darstellung (Eng.: relative description): Die unabhängigen Variablen sind die gegenwärtige Position $$x und eine variable Zeit $\tau$. Diese variable Zeit $\tau$ ist der Zeitpunkt, zu dem das Teilchen einen andere Position innehatte, z.B. $$ξ. Die Bewegung wird mit $$ξ als abhängige Variable beschrieben, z.B., $$ξ=χ_t (x,τ), wo der Index $t$ an $$χ_t betonen soll, daß die Referenzkonfiguration die Konfiguration zum Zeitpunkt $t$ ist.

Die materielle Darstellung bezieht sich also auf das Teilchen $X$, so daß die Bewegung $$x = x(X,t) symbolisch den Ort $$x des Teilchens zur Zeit $t$ angibt. Es kommt nach [3] häufiger zur Verwechslung oder Vermischung von materieller und Referenz-Darstellung, da die Position des Teilchens $$X in der Referenzkonfiguration häufig als Bezeichnung für das Teilchen selbst verwendet wird. Es wird dann von dem ``Teilchen $$X'' gesprochen. Einer theoretischen Trennung muß man sich aber bewußt sein. Die Referenz-Darstellung bezieht die Bewegung auf eine Referenz-Konfiguration, in der das Teilchen $X$ die Position $$X innehat. Wie oben erwähnt, ist das in der Elastizitätstheoie häufig der unbelastete Zustand, in den der Körper nach Entlastung wieder zurückkehrt. In den meisten Fällen wird diese Referenzkonfiguration zum Zeitpunkt $t=0$ gewählt (Lagrangesche Darstellung). Der Sprachgebrauch ist dann:'' $$x ist der ORT des Teilchens $$X zur Zeit $t$''. Gemeint ist: ``$$x ist zur Zeit $t$ die Position des Teilchens, welches in der Referenzkonfiguration die Position $$X besetzt hat''. Wir schreiben in kartesischen Koordinaten:

$$x =x(X,t)&thicksp;, &quad;x_i=x_i(X_j,t)=x_i(X₁,X₂,X₃,t) &thicksp;,

oder in allgemeinen Koordinaten in kontravarianter Darstellung der Komponenten:

$$x =x(X,t)&thicksp;, &quad;wⁱ=wⁱ(W^j,t)=wⁱ(W¹,W²,W³,t) &thicksp;,

wobei die $X$_i oder $Wi$ die materiellen Koordianten darstellen, d.h, die Koordinaten der Position des Teilchens in der Referenz-Konfiguration, während die $x$_i oder $wi$ die räumlichen Koordinaten sind, die den Ort $$x des Teilchens zur Zeit $t$ angeben. Die Schreibweise, $$x als Funktionsausdruck mit den Argumenten $$X und $t$, gleichzeitig aber auch für den Funktionswert (linke Seite) zu verwenden, ist in der Literatur üblich. Man kann das durch ein anderes Funktionssymbol umgehen.
Die räumliche Darstellung oder Eulersche Darstellung dagegen bezieht sich auf einen bestimmten räumlichen Bereich und ist damit in der Fluidmechanik bevorzugt verwendet.
Ist die Bewegung bekannt, so kann die Geschwindigkeit $$u als partielle Ableitung nach der Zeit bestimmt werden. Dabei ist $$X konstant zu halten, gleiches gilt für die Beschleunigung eines Teilchens:

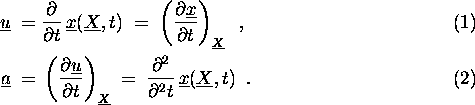
Diese Ableitungen sind von denen mit konstantem $$x unbedingt zu unterscheiden! Hierbei handelt es ich um lokale Änderungen, so ist z.B.

u&pd;t} }_x&thicksp; =&thicksp; {&pd;²&pd;² t}   x(x,t)&thicksp; &thicksp;

keine Beschleunigung (eines Teilchens), sondern die lokale Änderung der Geschwindigkeit.
Für die substantielle oder materielle Zeit-Ableitung in räumlichen Koordinaten wird häufig eine Rechenvorschrift benötigt, weil die Referenz- oder Lagrangesche Darstellung der Bewegung nicht bekannt ist, aber für die Berechnung von $$u und $$a notwendig ist. Ist aber eine eindeutige Funktion $$x(X,t) gegeben, so gilt nach der Kettenregel mit $f=g($X,t)=f(x(X,t),t), wobei aber $g($X,t) nicht bekannt ist:

_X= {({&pd;f&pd;t}}_x+ {&pd;f&pd;x_i} {({&pd;x_i&pd;t}}_X&thicksp;&thicksp;,

mit

_i&pd;t}}_X=u_i&thicksp;&thicksp;,

der Geschwindigkeit.
Für die substantielle Ableitung sind folgende Schreibweisen in Verwendung:

_X = f = {D&thicksp;fD&thicksp;t} = {d&thicksp;fd&thicksp;t},

für die lokale zeitliche Änderung schreiben wir:

_x = {&pd;f&pd;t}

und die Ableitung von $f$ bezüglich der räumlichen Koordinaten $x$_i wird als Gradient geschrieben, der bei Tensorkomponenten mit der kovarianten Ableitung zu bilden ist, so daß man Gl. 8 wie folgt umschreiben kann:

ugrad  f,

wobei die kovariante Ableitung in Indexschreibweise in allgemeinen Koordinaten wie folgt ausgeschrieben wird:

_X= {({&pd;f&pd;t}}_x+ f|_i {({&pd;wⁱ&pd;t}}_X&thicksp;&thicksp;.

Die materielle oder substantielle Ableitung einer Größe setzt sich also aus einer lokalen Änderung an einem Ort (erster Term) und einer örtlichen Änderung durch Bewegung des Teilchens zusammen (zweiter Term, konvektiver Anteil). Die Größe $f$ kann hierbei ein Skalar, einen Tensor oder eine Tensorkoordinate darstellen. In [7] sind die verschiedenen Ableitungen und Differentiale sowie Transportgleichungen erklärt und hergeleitet.
Zur kovarianten Ableitung eines Skalars sei noch kurz gesagt, daß sie der partiellen Ableitung nach den Koordinaten entspricht. Für Tensoren höher als nullter Stufe gilt:

$a$_l....m^i....j|_k&thicksp;=&thicksp;a_l....m^i....j,_k&thicksp; +&thicksp; Γⁱ_nka_l....m^n....j&thicksp;+&thicksp;..... +&thicksp; Γ^j_nka_l....m^i....n -&thicksp; Γⁿ_lka_n....m^i....j&thicksp;-&thicksp;..... -&thicksp; Γⁿ_mka_l....n^i....j&thicksp;,

wobei der erste Term die partielle Ableitung der Tensorkoordinate ist. In symbolischer Schreibweise schreibt man ebenfalls eine Komma für die partielle Ableitung der Tensoren selbst, die man dann mit der kovarianten Ableitung übersetzt, wie an Hand der folgenden Darstellungsgleichung für einen Tensor 2. Stufe deutlich wird:

$$a,_k&thicksp;=&thicksp; a^ij|_k&thicksp;g_i&thicksp;g_j&thicksp;=&thicksp;aⁱ_{&thicksp;&thicksp;j}|_k&thicksp;g_i&thicksp;g^j&thicksp;= &thicksp; .....

Die Christoffel-Symbole $\Gamma i$_nk sind dabei eine Abkürzung für

$\Gamma m$_ij&thicksp;=&thicksp;{&pd;² x_k&pd;wⁱ&pd;w^j} {&pd;w^m&pd;x_k},

wenn die Basis $$g_i&thicksp;=&thicksp;g_ijg^j bezüglich kartesischer Koordinaten gegeben ist, was meistens der Fall ist. Sind die $wi$ geradlinige, speziell kartesische Koordinaten, dann verschwinden die Christoffel-Symbole. Sie werden am einfachsten mit den Metrikkoeffizienten $g$_ij&thicksp;=&thicksp;g_ig_j oder gⁱg^j der Basis, in der bezüglich der Koordinaten abzuleiten ist, berechnet, siehe [8].
Ziel der Implementierung ist eine beliebige Lagrangesche Eulersche Formulierung (ALE, arbitrary Lagrangian Eulerian), wobei in den Strukturbereichen die Langrangesche Darstellung verwendet wird, indem die Gitter den Bewegungen des Materials folgen, während in den Strömungsbereichen die Eulersche Darstellung Anwendung findet.