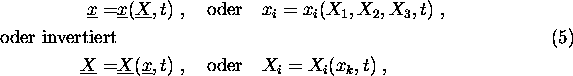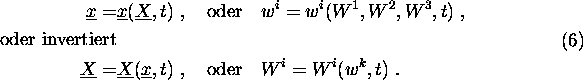Die Verzerrungstensoren

  
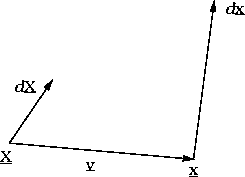
Abbildung 1: Materieller Vektor dX, Bewegung in neue Position dx

In der Abbildung 1 ist eine beliebige Veränderung eines materiellen Vektorelementes $d$X durch das Verschiebungsfeld $$v zu einer anderen Lage $d$x dargestellt. Es gibt viele verschiedene Definitionen für endliche Verformungen und Verzerrungen, die sich in zwei Arten einteilen lassen (siehe [3], Seite 155):

• Definitionen auf der Basis der unverformten Konfiguration: Verwendung der materiellen Koordinaten der unverformten Konfiguration, als Lagrangesche Formulierung oder Darstellung bezeichnet.
• Definitionen auf der Basis der verformten Konfiguration: Verwendung der räumlichen Koordinaten in der verformten Konfiguration, Eulersche Darstellung genannt.

Im folgenden sollen die vier grundlegenden Tensoren in beiden Darstellungen angegeben werden, eine ausführliche Beschreibung entnehme man u.a [3, 7]. Diese Tensoren sind der Deformationsgradient, dessen Transponierter, der Verformungstensor und der Verzerrungstensor. Der Deformationsgradient ist am einfachsten mit den Verformungsgleichungen 22 zu definieren und enthält mehr Information über die Bewegung als die anderen beiden, was jedoch ein Nachteil sein kann. In kartesischen Koordinaten sind die Verformungsgleichungen:
 
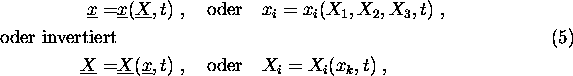
in allgemeinen Koordinaten schreibt man:
 
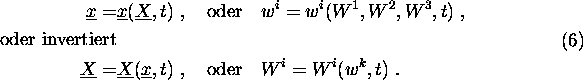
Der Nachteil hat seine Ursache darin, daß der Deformationsgradient sowohl die Rotation als auch die Deformation beschreibt, so daß Erhaltungsgleichungen, die mit diesem Tensor gebildet werden, so formuliert werden müssen, daß sich keine Spannungen auf Grund von Starrkörperdrehungen ergeben. Der Verzerrungstensor dagegen verschwindet bei Starrkörperdrehungen, so daß eine simple lineare, homogene Spannungs-Verzerrungs-Gleichung diese Forderung erfüllt. Die Lagrangesche Darstellung erscheint in der Elastizitätstheorie die geeignetere zu sein, weil es generell einen unverformten oder unbelasteten Zustand gibt, in den der Körper bei Entlastung zurückkehrt. Aber die Gleichgewichtsbedingungen und Spannungs-Verzerrungs-Zusammenhänge müssen in der verformten oder momentanen Konfiguration erfüllt werden. In einer solchen Gleichung müssen dann entweder die Spannungen zurück auf das unverformte System, oder die Verzerrungen auf das verformte System bezogen werden, um für alle Tensoren in einer Gleichung dasselbe Bezugssystem zu haben. Dies ist unter anderem auch Voraussetzung für die ''Übersetzung'' von symbolischer in Index-Schreibweise, [8].
Der Deformationsgradient $$F wird bezüglich der unverformten Konfiguration formuliert (erster Teil von Gleichung 22):

$d$x&thicksp;=&thicksp;Fd X und d x&thicksp;=&thicksp; d X F^T &thicksp;.

Es ist anzumerken, daß der Deformationsgradient zwar ein Tensor ist, aber keinesfalls ein Gradient in herkömmlichen Sinne der Definition eines Gradienten, siehe [7]. Darauf wird nicht in jeder Literaturstelle hingewiesen. Bei kartesischen Koordinaten ist diese Unterscheidung nämlich nicht notwendig, müsste formal korrekt aber bei einer Notation in symbolischer Schreibweise, wie in [3], Seite 156, erfolgt, beachtet werden. In kartesischen Basen schreiben wir:

$dx$_k={&pd;x_k&pd;X_l}&thicksp;dX_l ,

in allgemeinen Koordinaten:

woran man erkennen kann, daß es sich nicht um einen Gradienten handelt, da dann die kovariante Ableitung nach den Koordinaten verwendet werden müßte. In räumlichen Koordinaten oder Eulerscher Formulierung (zweiter Teil von Gleichung 22) schreiben wir:

$d$X&thicksp;=&thicksp;F^-1d x und d X&thicksp;=&thicksp; d x (F^-1)^T &thicksp;,

somit in kartesischen Koordinaten:

$dX$_k={&pd;X_k&pd;x_l}&thicksp;dx_l .

Es handelt sich bei $$F und $$F^-1 um zueinander inverse Tensoren. Der Deformationsgradient beschreibt die Deformation in einem infinitesimalen Gebiet um ein Teilchen, seine Komponenten selbst hingegen sind endlich.
Über den Deformationsgradienten können die in Tabelle 1 zusammengefassten, generell gültigen Aussagen gemacht werden. Es ist zu erkennen, daß der Deformationsgradient bei Starrkörperrotationen nicht verschwindet, weswegen andere Tensoren definiert werden, siehe z.B. Gleichung 29 und 30. Dies kann man ebenfalls über eine Aufteilung in symmetrische und antimetrische Anteile erreichen, denn eine Starrkörperrotation ist duch einen antimetrischen Tensor beschrieben. Einen antimetrischen Anteil gibt es bei einem symmetrischen Tensor nicht, $$E und $$E* aber sind per Definition symmetrisch.

 

Verformungsart Aussage über $$F

Translation, $v$_i=const. $F$_ij=δ_ij

Rotation, starre Bewegung $F$_ij ist orthogonal

Verzerrung $F$_ij ist symmetrisch

Dilatation (Richtung bleibt erhalten) $F$_ij ist isotrop

Distorsion (Volumen bleibt erhalten) $det\; F$_ij&thicksp; =&thicksp; 1

 

Die Verzerrungstensoren $$E und $$E* sind so definiert, daß sie die Änderung des Längenquadrats des materiellen Vektors $d$X angeben. In Lagrangescher Darstellung:

X E dX,

oder in Eulerscher Darstellung:

x E* dx.

Zum Schluß seien noch die Verformungstensoren $$C und $$B^-1 betrachtet, denn sie sind eng mit dem klassischen Verzerrungstensor verknüpft. Anstelle der Längenänderung gibt der Greensche Deformationstensor (oder Greenscher Verzerrungstensor oder rechter Cauchy-Green Tensor) $$C die neue verformte Länge $(ds)2$ des Elements, in das $d$X bei der Verformung übergeht, bezogen auf das unverformte System an. Der Inverse des Cauchyschen Verformungstensors (oder Cauchyscher Verzerrungstensor oder linker Cauchy-Green Tensor) $$B^-1 oder $$c dagegen gibt das Anfangslängenquadrat $(dS)2$ eines Elementes $d$x im verformten System an:
 
Beim Vergleich mit 29 und 30 erhält man:

E&thicksp;=&thicksp; C &thicksp;-&thicksp;δ und 2&thicksp;E*&thicksp;=&thicksp;δ&thicksp;-&thicksp; B^-1&thicksp;.

Die Deformationstensoren werden zum Einheitstensor, wenn es keine Verzerrungen gibt. Mit den Zusammenhängen 24 und 25 und den Längen x d x und X d X folgt:

$$C&thicksp;=&thicksp;(F)^T F und B^-1&thicksp;=&thicksp;(F^-1)^T F^-1&thicksp;,

damit aus 32 schließlich:

$$E&thicksp;=&thicksp; {12}{( (F)^T F&thicksp;-&thicksp;δ } und E*&thicksp;=&thicksp; {12}{( δ&thicksp;-&thicksp; (F^-1)^T F^-1 }.

$$C und $$E sind symmetrische Tensoren und ihre Hauptachsen fallen zusammen, [3]. Gleiches gilt für $$B^-1 und $$E*, ihre Hauptachsen fallen im Raumpunkt $$x zusammen, sind im allgemeinen aber nicht parallel zu den Hauptachsen von $$C und $$E im Punkte $$X. Die Eigenwerte von $$C und $$B^-1 sind alle positiv, was aus den Definitionsgleichungen 31 folgt.
Wird eine Bewegung, dargestellt in kartesischen Koordinaten, gegeben durch:

$x$_i&thicksp;=&thicksp;X_i&thicksp;+&thicksp;v_i mit v_i&thicksp;=&thicksp;v_i(X_k,t)&thicksp;,

so erhält man dann die kartesischen Koordinaten

$E$_ij&thicksp;=&thicksp;{12}&thicksp;{( {&pd;v_i&pd;X_j}&thicksp;+&thicksp; {&pd;v_j&pd;X_i}&thicksp;+&thicksp; {&pd;v_k&pd;X_i}&thicksp; {&pd;v_k&pd;X_j} }&thicksp;.

Sind die Ableitungen der Verschiebungen $v$_i in Bezug auf die materielle Basis klein gegenüber eins, so können die Produktterme gegenüber den linearen Termen vernachlässigt werden. Bei kleinen Verzerrungen ist das zulässig. Dies ist z.B. bei elastischen Verformungen von Metall der Fall, [3]. Plastische Verformungen von Metall und gummielastisches Verhalten erlauben diese Vereinfachungen nicht mehr.
Analog kann man die Koordinaten von $$E* durch Verschiebungsableitungen ausdrücken mit den räumlichen, kartesischen Koordinaten

$X$_i&thicksp;=&thicksp;x_i&thicksp;-&thicksp;v_i mit v_i&thicksp;=&thicksp;v_i(x_k,t)&thicksp;,

so daß man die kartesischen Koordinaten:

$E$_ij*&thicksp;=&thicksp;{12}&thicksp;{( {&pd;v_i&pd;x_j}&thicksp;+&thicksp; {&pd;v_j&pd;x_i}&thicksp;-&thicksp; {&pd;v_k&pd;x_i}&thicksp; {&pd;v_k&pd;x_j} }&thicksp;

erhält. Eine Vernachlässigung der quadratischen Terme ist unter oben angegebenen Voraussetzungen ebenfalls möglich, zu beachten ist aber, daß bezüglich der Raumkoordinaten $x$_i abgeleitet wird.
Die $E$_ij⁴⁴⁵¹* werden Eulersche Verzerrungskomponenten und die $E$_ij Lagrangesche Verzerrungskompneneten genannt. Wenn die Verschiebungen und Verschiebungsableitungen hinreichend klein sind, wie z.B. in der klassischen linearisierten Elastizitätstheorie vorausgesetzt, dann ist diese Unterscheidung bei den Verzerrungstensorkoordinaten nicht mehr notwendig. Man verwendet dann häufig als Bezeichnung für die Verzerrungstensorkomponenten $\epsilon$_ij. Anzumerken ist noch, daß es sich bei den Komponenten um exakte Ausdrücke handelt - höhere als qudratische Terme gibt es nicht - so daß dies die kompletten Tensoren für endliche Verzerrungen sind, keine Approximationen zweiter Ordnung!