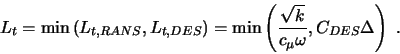

Nächste Seite: Transition
Aufwärts: Numerisches Verfahren
Vorherige Seite: Simulation instationärer turbulenter Strömungen
Simulationen turbulenter Strömungen können auf der Basis
von URANS-Verfahren gelöst werden.
Dabei können lineare Ein- und Zweigleichungsturbulenzmodelle sowie
explizite oder implizite Reynoldsspannungsmodelle zum Einsatz
kommen, die in Low- oder High-Re-Formulierung zur Verfügung stehen.
In den meisten Simulationen kommt das LLR-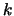 -
-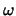 Modell [18]
zum Einsatz.
Die Probleme statistischer Turbulenzmodelle bei der Wiedergabe
stark instationärer Strömungen können durch die Verwendung hochauflösender
Verfahren (LES, DNS) vermieden werden. Um den damit verbundenen extremen
Rechenaufwand zu vermeiden, sind in letzter Zeit hybride Methoden populär
geworden. Diese lokal adaptiven Techniken versuchen, die Vorteile
des URANS-Ansatzes bei Grenzschichtströmungen, die in der Regel mit sehr
kleinen turbulenten Zeitmaßen verbunden sind, mit denen der LES-Verfahren bei
starker Ablösung, freien Scherströmungen und Nachläufen zu kombinieren.
Mit Hilfe der DES
können ähnlich wie bei einer LES die energiereichen
turbulenten Strukturen in ihrer zeitlichen und räumlichen Entwicklung
aufgelöst werden, ohne jedoch auf die hohe räumliche Auflösung
in Wandnähe angewiesen zu sein.
Die als DES [16], VLES [19] oder LNS
[20] bekannten Verfahren kombinieren den statistischen Ansatz
eines Turbulenzmodells mit dem Konzept der Auflösung großer Wirbel
einer LES. Dadurch wird der modellierte Bereich des Turbulenzmodells
beschränkt und eine spektrale Überlappung verhindert.
Das Umschalten erfolgt in Abhängigkeit vom
turbulenten Längenmaß.
Zur besseren
Vergleichbarkeit zwischen den Ergebnissen der unterschiedlichen Ansätze
wird die Implementierung auf Basis des LLR-Modells gewählt.
Dabei wird die Dissipation in der Transportgleichung der turbulenten kinetischen
Energie in Abhängigkeit vom turbulenten Längenmaß formuliert.
Modell [18]
zum Einsatz.
Die Probleme statistischer Turbulenzmodelle bei der Wiedergabe
stark instationärer Strömungen können durch die Verwendung hochauflösender
Verfahren (LES, DNS) vermieden werden. Um den damit verbundenen extremen
Rechenaufwand zu vermeiden, sind in letzter Zeit hybride Methoden populär
geworden. Diese lokal adaptiven Techniken versuchen, die Vorteile
des URANS-Ansatzes bei Grenzschichtströmungen, die in der Regel mit sehr
kleinen turbulenten Zeitmaßen verbunden sind, mit denen der LES-Verfahren bei
starker Ablösung, freien Scherströmungen und Nachläufen zu kombinieren.
Mit Hilfe der DES
können ähnlich wie bei einer LES die energiereichen
turbulenten Strukturen in ihrer zeitlichen und räumlichen Entwicklung
aufgelöst werden, ohne jedoch auf die hohe räumliche Auflösung
in Wandnähe angewiesen zu sein.
Die als DES [16], VLES [19] oder LNS
[20] bekannten Verfahren kombinieren den statistischen Ansatz
eines Turbulenzmodells mit dem Konzept der Auflösung großer Wirbel
einer LES. Dadurch wird der modellierte Bereich des Turbulenzmodells
beschränkt und eine spektrale Überlappung verhindert.
Das Umschalten erfolgt in Abhängigkeit vom
turbulenten Längenmaß.
Zur besseren
Vergleichbarkeit zwischen den Ergebnissen der unterschiedlichen Ansätze
wird die Implementierung auf Basis des LLR-Modells gewählt.
Dabei wird die Dissipation in der Transportgleichung der turbulenten kinetischen
Energie in Abhängigkeit vom turbulenten Längenmaß formuliert.
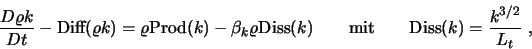 |
(1) |
wobei das Längenmaß 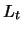 den eigentlichen Schalter zwischen RANS und LES
darstellt:
den eigentlichen Schalter zwischen RANS und LES
darstellt:
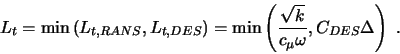 |
(2) |
Die Definition des Längenmaßes 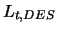 orientiert sich am
Ansatz der LES mit der Konstanten
orientiert sich am
Ansatz der LES mit der Konstanten 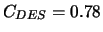 nach Strelets
[17] und der lokalen Auflösung des Gitters:
nach Strelets
[17] und der lokalen Auflösung des Gitters:
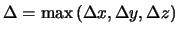 .
Sowohl für die Untersuchung der Rückstromklappen als auch die der
Gurney-Flaps wurden zusätzlich Grobstruktursimulationen durchgeführt.
.
Sowohl für die Untersuchung der Rückstromklappen als auch die der
Gurney-Flaps wurden zusätzlich Grobstruktursimulationen durchgeführt.


Nächste Seite: Transition
Aufwärts: Numerisches Verfahren
Vorherige Seite: Simulation instationärer turbulenter Strömungen
Markus Schatz
2004-01-28