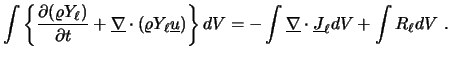Spezieserhaltung

Bei der numerischen Simulation von Mehrphasenströmungen oder chemischen Reaktionen muß die Erhaltung der einzelnen Komponenten (Spezies) sichergestellt werden. In diesem Fall wird als transportierte Größe der Massenbruch, d.h. der relative Anteil einer bestimmten Komponente an der Gesamtmasse betrachtet:

$$\int \left\{ \frac{\partial (\varrho Y_{\ell})}{\partial t} + \un... ...= -\int \underline{\nabla} \cdot \underline{J}_{\ell} dV + \int R_{\ell} dV \ .$$ (2.16)

$$Y_{\ell} = \ \ \ell$$

$$R_{\ell} = \$$

$$\underline{J}_{\ell} = \quad J_{i \ell}= -\Gamma \frac{\partial Y_{\ell}}{\partial x_i} \ .$$

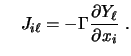In differentieller Form lautet die Erhaltungsgleichung für eine Komponente damit:

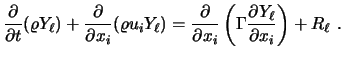$${\partial \over \partial t} (\varrho Y_{\ell}) + {\partial \over ... ..._i} \left( \Gamma {\partial Y_{\ell} \over \partial x_i} \right) + R_{\ell} \ .$$ (2.17)