Es soll untersucht werden, in welcher Weise sich eine beliebige
Eigenschaft ![]() (Impuls, Dichte, etc.) eines flüssigen
''Körpers'', also eines materiellen Volumens
(Impuls, Dichte, etc.) eines flüssigen
''Körpers'', also eines materiellen Volumens ![]() , ändert.
Das Problem liegt hierbei in der Tatsache, daß ein solches
Volumen zwar immer von denselben Teilchen gebildet wird, seine
Gestalt und räumliche Lage sich jedoch fortlaufend ändern.
, ändert.
Das Problem liegt hierbei in der Tatsache, daß ein solches
Volumen zwar immer von denselben Teilchen gebildet wird, seine
Gestalt und räumliche Lage sich jedoch fortlaufend ändern.
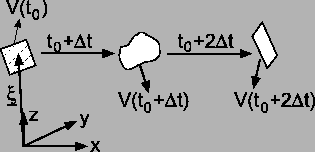
 |
(2.1) |
![]() 1 symbolisiert hier eine allgemeine rechte Seite, die in der
Regel aus sogenannten Quelltermen zur Erzeugung oder Vernichtung
von
1 symbolisiert hier eine allgemeine rechte Seite, die in der
Regel aus sogenannten Quelltermen zur Erzeugung oder Vernichtung
von ![]() besteht.
Da das Volumen, d.h. die Integrationsgrenzen, ebenfalls von der Zeit
abhängt, muß man die Leibnitzsche Regel anwenden und notiert
besteht.
Da das Volumen, d.h. die Integrationsgrenzen, ebenfalls von der Zeit
abhängt, muß man die Leibnitzsche Regel anwenden und notiert
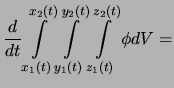 |
![$\displaystyle \int \limits_{V(t_0)} \frac{\partial \phi}{\partial t} dV
+ \left...
...( \phi
\frac{\partial x}{\partial t} \right) dA_x \right]_{x_1(t_0)}^{x_2(t_0)}$](img27.png) |
||
![$\displaystyle \left[ \int \limits_{A_y(t_0)} \left( \phi
\frac{\partial y}{\par...
...hi
\frac{\partial z}{\partial t} \right) dA_z \right]_{z_1(t_0)}^{z_2(t_0)}
\ ,$](img29.png) |
(2.2) |
und damit
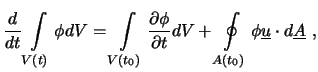 |
(2.3) |
wobei
![]() die
Geschwindigkeit2
des Volumens bzw. der
Teilchen, die dieses Volumen bilden,
angibt und
die
Geschwindigkeit2
des Volumens bzw. der
Teilchen, die dieses Volumen bilden,
angibt und
![]() die Oberfläche des Volumens darstellt.
die Oberfläche des Volumens darstellt.
Es ergibt sich das Reynoldsche Transporttheorem
Mit Hilfe des Gaußschen Satzes
![]() erhält man die konservative Form der Erhaltungsgleichung:
erhält man die konservative Form der Erhaltungsgleichung:
Die Verwendung der substantiellen Ableitung 3führt auf eine kompakte Formulierung:
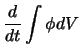 |
![$\displaystyle \int \left[ \frac{\partial \phi}{\partial t}
+\underline{\nabla} \cdot ( \phi \underline{u} ) \right] dV$](img44.png) |
||
![$\displaystyle \int \left[
\frac{\partial \phi}{\partial t}
+ \underline{\nabla} \phi \cdot \underline{u}
+ \phi \underline{\nabla} \cdot \underline{u} \right] dV$](img45.png) |
|||
![$\displaystyle \int \left[ \frac{D \phi}{Dt}
+ \phi \underline{\nabla} \cdot \underline{u}
\right] dV \ .$](img46.png) |
(2.6) |