Die Hinzunahme zweier weiterer Nachbarn ![]() und
und ![]() (bottom, top) ergibt die Diskretisierungsgleichung:
(bottom, top) ergibt die Diskretisierungsgleichung:
| (4.42) |
mit
 |
|||
 |
|||
 |
|||
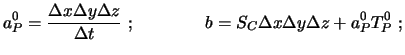 |
(4.43) |
Zur physikalischen Signifikanz der Koeffizienten:
Die Nachbarkoeffizienten können interpretiert werden als
Leitfähigkeiten zwischen ![]() und dem jeweiligen
Nachbarpunkt.
und dem jeweiligen
Nachbarpunkt.
![]() ist die interne Energie (pro
ist die interne Energie (pro ![]() ) im
Kontrollvolumen zur Zeit
) im
Kontrollvolumen zur Zeit ![]() . Der Term
. Der Term ![]() enthält diese innere Energie und
den Wärmeerzeugungsanteil aus
enthält diese innere Energie und
den Wärmeerzeugungsanteil aus ![]() .
.
Der zentrale Koeffizient ![]() ist die Summe aller
Nachbarkoeffizienten (einschließlich des Zeitnachbarkoeffizienten
ist die Summe aller
Nachbarkoeffizienten (einschließlich des Zeitnachbarkoeffizienten
![]() ) und des Beitrags des linearen Quellterms.
) und des Beitrags des linearen Quellterms.