Die Wahl geeigneter anderer Koordinaten kann wesentliche Vereinfachungen mit sich bringen (Reduktion der Anzahl unabhängiger Variabler
Unabhängige Variablen sind im allgemeinen Fall die Zeit
Die Wahl geeigneter anderer Koordinaten kann wesentliche
Vereinfachungen mit sich bringen (Reduktion der Anzahl unabhängiger
Variabler ![]() Gitterpunkte).
Gitterpunkte).
Beispiele:
Auch die geeignete Wahl abhängiger Variablen kann eine
Reduktion des Rechenaufwands bewirken.
Dimensionslose Variable
Beispiel: eindimensionale Wärmeleitung:

Dimensionsbehaftete Variable: macht viele Lösungen erforderlich;
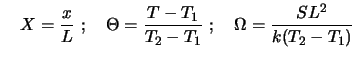
dann
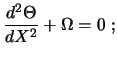
Das Problem wird nur noch durch einen Parameter
![]() beschrieben.
beschrieben.
Für jeden Problemtyp ist ein unterschiedlicher Satz von Parametern notwendig. Die Parameter sind jedoch nicht universell definiert:
Eine Alternative zum obigen Beispiel:
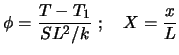
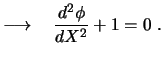
Die Differentialgleichung enthält jetzt keinen Parameter
mehr! Der Parameter steht jetzt in der Randbedingung:
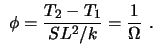 |
Wir werden im folgenden von den dimensionsbehafteten
Gleichungen und Größen ausgehen. Die Terme der
Differentialgleichungen haben dann eine anschauliche
physikalische Bedeutung.