



Nächste Seite: Nichtlinearität
Aufwärts: Variable (Wärme-) Leitfähigkeit
Vorherige Seite: Variable (Wärme-) Leitfähigkeit
Inhalt
Für kleine Änderungen sind beide gleich gut geeignet.
Behandlung der Grenzfälle:
- 1)
-
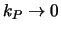
- harmonisch:
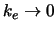
(arithmetisch:
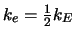 )
)
- Der Wärmefluß am Rand eines Isolators wird beim harmonischen Mittel
Null, wie es sein sollte. Das arithmetische Mittel ergibt Fluß
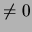 .
.
- 2)
-
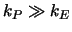
- harmonisch:
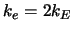
(arithmetisch:
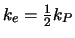 )
)
- Die Wandleitfähigkeit
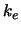 ist nicht von
ist nicht von 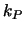 abhängig.
Ein Material hoher Wärmeleitfähigkeit bietet keinen Widerstand im
Vergleich zum Material
abhängig.
Ein Material hoher Wärmeleitfähigkeit bietet keinen Widerstand im
Vergleich zum Material 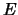 (das arithmetische Mittel würde nur den
Effekt von
(das arithmetische Mittel würde nur den
Effekt von 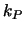 auf
auf 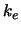 widerspiegeln). Der Faktor 2 kommt aus
der Verwendung eines nominellen Gradienten
widerspiegeln). Der Faktor 2 kommt aus
der Verwendung eines nominellen Gradienten
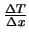 statt des wirklichen Gradienten:
statt des wirklichen Gradienten:
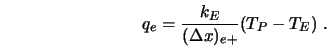 |
(4.12) |
Abbildung:
Interpolation bei extrem verschiedenen Wärmeleitfähigkeiten
![\includegraphics*[width=6.5cm, angle=0]{Abb/fvm4_3.eps}](img258.png) |
- Einen Temperaturabfall gibt es lediglich im Kontrollvolumen
 ;
das Kontrollvolumen
;
das Kontrollvolumen  ist praktisch isotherm.
ist praktisch isotherm.
- Fazit: Das harmonische Mittel gibt bessere Ergebnisse
für stark veränderliches
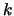 . Die Formel hat einige weitere
nützliche Eigenschaften, die später erläutert werden.
. Die Formel hat einige weitere
nützliche Eigenschaften, die später erläutert werden.
Damit haben wir auch die Profilannahme geändert:
Abbildung:
Veränderte Profilannahmen
|
|




Nächste Seite: Nichtlinearität
Aufwärts: Variable (Wärme-) Leitfähigkeit
Vorherige Seite: Variable (Wärme-) Leitfähigkeit
Inhalt
Ulf Bunge
2003-10-10
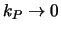
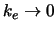
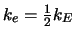 )
)
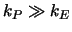
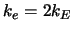
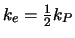 )
)