Bei variabler Leitfähigkeit ist i.a. der Wert von ![]() nur an
den Gitterpunkten
nur an
den Gitterpunkten ![]() usw. bekannt. Benötigt wird eine
Vorschrift zur Berechnung von z.B.
usw. bekannt. Benötigt wird eine
Vorschrift zur Berechnung von z.B. ![]() aus diesen Werten. Eine simple
lineare Interpolation zwischen Gitterpunkten ist z.B.:
aus diesen Werten. Eine simple
lineare Interpolation zwischen Gitterpunkten ist z.B.:
| (4.5) |
mit
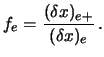 |
(4.6) |
Für ![]() in der Mitte zwischen
in der Mitte zwischen ![]() und
und ![]() ist
ist ![]() ,
und
,
und ![]() ist das arithmetische Mittel aus
ist das arithmetische Mittel aus ![]() und
und ![]() .
Dies erweist sich in bestimmten Fällen als nachteilig, insbesondere
bei abrupten Änderungen in inhomogenen Medien.
.
Dies erweist sich in bestimmten Fällen als nachteilig, insbesondere
bei abrupten Änderungen in inhomogenen Medien.
Eine bessere Alternative folgt aus der Überlegung, daß
nicht der lokale Wert der Leitfähigkeit am Kontrollvolumen-Rand
interessiert, sondern in erster Linie eine gute Darstellung des
Wärmeflusses ![]() am Rand gesucht ist:
am Rand gesucht ist:
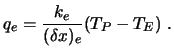 |
(4.7) |
Betrachtet man jedes KV als jeweils gefüllt mit einem Material
konstanter Leitfähigkeit, dann ergibt sich aus einer lokalen
Betrachtung:
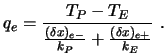 |
(4.8) |
Damit ist
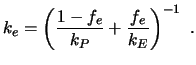 |
(4.9) |
Falls ![]() wieder in der Mitte zwischen
wieder in der Mitte zwischen ![]() und
und ![]() liegt
liegt
![]() , dann ist
, dann ist
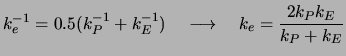 |
(4.10) |
Das ist das harmonische Mittel.
Damit ergibt sich für den Koeffizienten
![$\displaystyle a_E = \left[ {(\delta x)_{e-} \over k_P} + {(\delta x)_{e+} \over k_E} \right]^{-1}$](img247.png) |
(4.11) |
und somit ist
![]() die Summe der
Wärmeleitungswiderstände für das Material zwischen
die Summe der
Wärmeleitungswiderstände für das Material zwischen ![]() und
und ![]() .
.