![\includegraphics[width=0.90\textwidth]{skizze.eps}](skizze.gif)
|
The present numerical study is related to experimental investigations
by Tinapp [1] and Spang [7].
The test model is a generic two element high-lift configuration,
consisting of a NACA 4412 main airfoil and a NACA 4415 flap with
![]() relative chord length. Both profiles have bluff trailing
edges. A previous study [8] of a similar test case
showed that due to strong blocking the effect of the tunnel walls is
very important and needs to be considered. The main airfoil is mounted
at
relative chord length. Both profiles have bluff trailing
edges. A previous study [8] of a similar test case
showed that due to strong blocking the effect of the tunnel walls is
very important and needs to be considered. The main airfoil is mounted
at ![]() of the tunnel height (
of the tunnel height (![]() ), whereas the flap is
situated at a fixed position underneath the trailing edge of the main
airfoil, thus forming a gap of
), whereas the flap is
situated at a fixed position underneath the trailing edge of the main
airfoil, thus forming a gap of ![]() with an overlap of
with an overlap of
![]() (Fig.
(Fig. ![]() ). In the numerical study, the angle of
attack is fixed at
). In the numerical study, the angle of
attack is fixed at
![]() for the main airfoil and
for the main airfoil and
![]() for the flap.
for the flap.
The freestream velocity is
![]() corresponding to a
Reynolds-Number of
corresponding to a
Reynolds-Number of
![]() based on the main-airfoil chord.
Transition is fixed at the positions of turbulator strips at
4.5% chord on the main airfoil and 2.8% chord on the flap
according to the experimental setup.
based on the main-airfoil chord.
Transition is fixed at the positions of turbulator strips at
4.5% chord on the main airfoil and 2.8% chord on the flap
according to the experimental setup.
In the experiments [7] periodic oscillating pressure
pulses are generated externally by an electrodynamic shaker driving a
small piston. It results in an oscillating jet emanating perpendicular
to the chord from the narrow slot ![]() chord behind the flap leading
edge. This excitation is presumed to be completely two-dimensional
and it does not introduce extra mass-flux (zero-net-mass).
To model the excitation apparatus, a suction/blowing type boundary
condition is used. The perturbation to the flowfield is
introduced through the inlet-velocity
chord behind the flap leading
edge. This excitation is presumed to be completely two-dimensional
and it does not introduce extra mass-flux (zero-net-mass).
To model the excitation apparatus, a suction/blowing type boundary
condition is used. The perturbation to the flowfield is
introduced through the inlet-velocity ![]() to a small chamber
representing the excitation slot:
to a small chamber
representing the excitation slot:
| (1) |
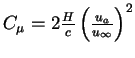 with
is the slot-width
with
is the slot-width