Discussion

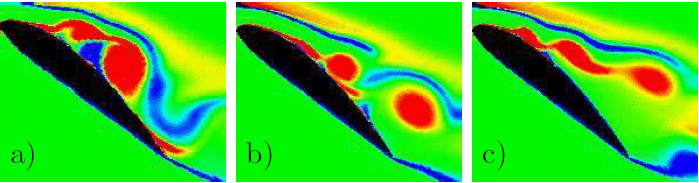
One of the results from simulations with different excitation frequencies and intensities is the difference in the size of detaching vorticies. In Tab. 2 the size of a pair of vortices $x_w/c_k$ is plotted.

Figure: Flowfield around flap represented by vorticity distribution for different excitation frequencies: a) $F^+ =0.26$, b) $F^+ =0.62$ and c) $F^+ =1.54$

$F^+$	0	0.26	0.62	1.54	0.51	0.51
$C_{\mu} \cdot 10^5$	0	50	50	50	25	100
$x_w/c_k$	0.9	0.83	0.50	0.40	0.51	0.43

Tab. 2 $\$ Size of detaching vorticies for different frequencies and intensities

Compared to the baseline case ($x_w/c_k=0.9$) the size of structures in the wake becomes smaller with increasing excitation frequency and high intensity. An optimum lift combined with minimum drag corresponds to smaller vorticies with roughly $x_w/c_k=0.5$.

As the predominant part of the lift of a high-lift configuration is generated by the main airfoil, the most important effect of periodic excitation is to change the flow direction at the main airfoil trailing-edge. By delaying separation on the flap the mean flow direction behind the trailing-edge is changed (Fig. ). Vortices are generated and transported downstream and interact with those vortices detaching from the main airfoil. The surface pressure and the lift coefficient are oscillating with the excitation frequency. Flow control with lower intensity means smaller vortices, which are able to penetrate the flap boundary-layer and the shear layer between freestream and reverse flow. However, larger vortices move away from the flap surface and are less effective. This may explain the small effect of low intensity excitation.

The flow separation is located in the turbulent part of the flow. However, turbulence intensity is very low at the separation point. One effect of periodic excitation is to transfer energy from the potential flow region into the boundary-layer. Steady simulations of turbulent flow with high turbulence intensity predict attached flow for high flap angles [8] stressing that high turbulence intensity can avoid flow separation on the flap.

For the flow without excitation the Strouhal number is $St=F^+ x_w / c_k \approx 0.4$. The approximation () indicates a factor of 10 between the resolved and the modelled time-scales. Due to periodic excitation ( $F^+=1.03, C_{\mu}=50 \cdot 10^{-5}$) the Strouhal number decreases to $St \approx 0.25$. In this case equation () leads to a factor of 20. To get a more reliable expression, the entire flow field is checked for the smallest occuring time-scales. In the case without excitation the resolved time-scale is $T_t=1/F^+ = 2.3$ and without excitation $T_t= 1.0$. For both cases the modelled non-dimensional time-scales remain between $T_m \approx 0.05 - 2$. Most critical areas are situated in the flap wake, in which in the present case the spectral gap disappears for high excitation frequencies. On the other hand the gap remains large enough in the main part of the flowfield. The realiability of the simulation and validity of RANS can be assumed.