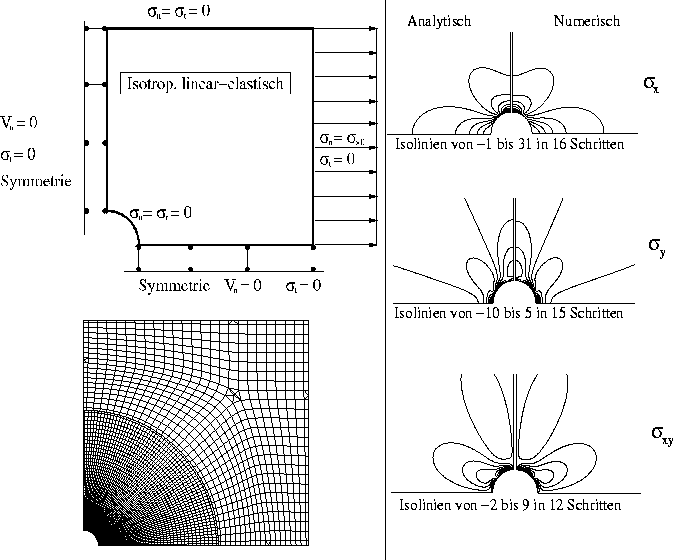
Abbildung 1: Prinzipskizze, Gitter (links) und Vergleich der Spannungen aus analytischer und numerischer Berechnung (rechts)
| Bearbeiter: | Ulf Bunge |
| Forschungsträger: | EU |
Notwendige und aus der Entwicklung von FEM-Programmen bekannte Tests [1] sind durchgeführt worden, wozu z.B. die korrekte und spannungsfreie Wiedergabe von Starrkörperverschiebungen oder die störungsfreie Berechnung elementarer Belastungszustände gehören.

Abbildung 1: Prinzipskizze, Gitter (links) und Vergleich der Spannungen aus analytischer
und numerischer Berechnung (rechts)
Zur weiteren Kontrolle ist ein Lastfall gerechnet worden, der einer analytischen Lösung zwar
zugänglich ist,
aber ein hochgradig nichtlineares Verhalten aufweist. Dies ist die Lochscheibe unter eichachsigem Zug,
siehe Abb.1.
Die analytische Lösung ist am einfachsten in Zylinderkoordinaten zu erhalten, siehe
[4, ].
Unter der Annahme isotropen Materials erhält man dabei eine Normalspannungsüberhöhung
an der Lochflanke um den Faktor 3 gegenüber der elementaren Belastung.
Die Ausnutzung der Symmetrie ist ein Test der implementierten Randbedingungen und erspart
Rechenzeit.
Als weitere Eigenschaft des Programmes ist die Berücksichtigung hängender Knoten
mit diesem Fall ebenfalls dokumentiert.
Die resultierenden Verschiebungen erfüllen die Randbedingungen, da jedoch
die analytische Lösung nur für die Spannungen vorliegt, ist ein Vergleich der Spannungen aus
analytischer
und numerischer Rechnung notwendig, wie in Abb.1 dargestellt.
Desweiteren sind Wärmeleitung nach Fourier und Verzerrungen infolge Temperaturveränderungen implementiert und getestet, wobei anisotropes Materialverhalten zugelassen wird.

Abbildung 2: Verformtes Gitter (links) und Detailansicht der Randbedingungen (rechts)
Ein weiterer Testfall lehnt sich an eine Rechnung aus [3] an.
Es handelt sich um einen
Gabelschlüssel, der an zwei Punkten im Maul festgehalten (modellhafte Abbildung der Kontaktpunkte beim
Festziehen einer Sechskanntmutter) und am Stielende mit einer Streckenlast beaufschlagt wird
(idealisierte Kraft z.B. durch
eine Hand). Das verformte Gitter ist in Abb. 2 dargestellt.
Es ist sehr fein und besteht aus fünf Blöcken, wobei die Blockgrenzen mit und ohne hängende
Knoten realisiert sind.
Es ist anzumerken, daß die Verformung stark verstärkt dargestellt wird, um sie sichtbar zu machen,
was auf Grund der Linearität des Problemes zu keiner Verfälschung führt. Die tatsächlichen
Verschiebungen sind kleiner und kaum sichtbar.