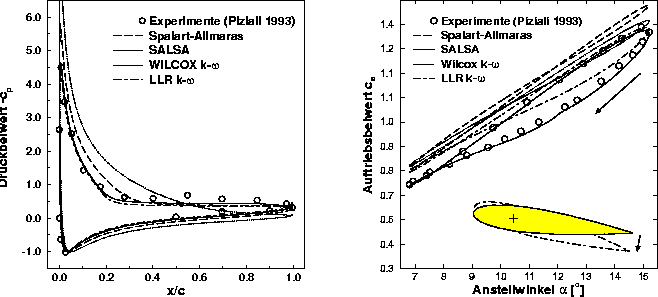
Abbildung: Vergleich der numerischen Ergebnisse unterschiedlicher Turbulenzmodelle links: Druckbeiwert bei rechts: Auftriebsbeiwert über Anstellwinkel für
| Bearbeiter: | Ulf Bunge, Markus Schatz, Thomas Rung |
| Forschungsträger: | DFG, EU |
Für die numerische Untersuchung solcher Phänomene kommen wegen der komplizierten Geometrien und der großen Reynoldszahlen nur Simulationen auf Basis der Reynolds-gemittelten Navier-Stokes Gleichungen mit statistischen Turbulenzmodellen in Frage. Ein solcher Ansatz ist zu vertreten, falls das turbulente Zeitmaß der Fluktuationsbewegungen deutlich kleiner ist als das charakteristische Strömungszeitmaß und die Zeitschrittweite . Außerdem gilt es zu untersuchen, inwieweit die relevanten physikalischen Vorgänge beim dynamischen Strömungsabriß von Reynolds-gemittelten Ansätzen und Turbulenzmodellen wiedergebeben werden können.
Die Behandlung der zeitlich veränderlichen Geometrie erfolgt einmal mit einem Gitter, das im Außenbereich unbeweglich ist, im Nahbereich des Tragflügelprofils eine Starrkörperbewegung ausführt und in dem Bereich dazwischen verformbar ist. Ein anderes Mal alternativ mit einem Gitter, daß sich starr mit dem Profil bewegt. In diesem Bereich wird das Gitter bei jedem Zeitschritt neu durch transfinite Interpolation erzeugt. Die Berücksichtigung der zeitlich veränderlichen Geometrie und Metrik ist durch ein von Demirdžić und Perić [1] vorgeschlagenes Verfahren, das jedem Gitterpunkt eine Geschwindigkeit zuweist, gegeben.

Abbildung: Vergleich der numerischen Ergebnisse unterschiedlicher
Turbulenzmodelle
links: Druckbeiwert
bei rechts: Auftriebsbeiwert
über Anstellwinkel für
Zunächst wird die stationäre Strömung um ein NACA0015 Tragflügelprofil untersucht. Für den Anstellwinkel ergibt der Vergleich mit experimentellen Ergebnissen [3], daß sich mit Hilfe der auf Nichtgleichgewichtszustände angepaßten Modelle LLR - und SALSA sowie eines MUSCL-Schemas zur Behandlung der konvektiven Flüsse die besten Resultate erzielen lassen. Nur hier kann die Strömungsablösung auf der Oberseite korrekt wiedergegeben werden (Abb. 1 links). Das gleiche Modell und Konvektionsschema wird deshalb auch für die folgenden instationären Strömungen verwendet.
Die Untersuchungen werden nun auf ein mit der Frequenz oszillierendes Profil erweitert: mit der reduzierten Frequenz . Bei einem Anstellwinkel, der sinusförmig um einen Mittelwert von bei einer Amplitude von schwankt, ergibt sich bereits eine deutlich Hysterese, d.h. der Auftriebsbeiwert ist bei steigendem Anstellwinkel größer als bei fallendem. Dieses Verhalten kann numerisch gut wiedergegeben werden und die Ergebnisse stimmen weitgehend mit den Experimenten überein (Abb. 1 rechts).
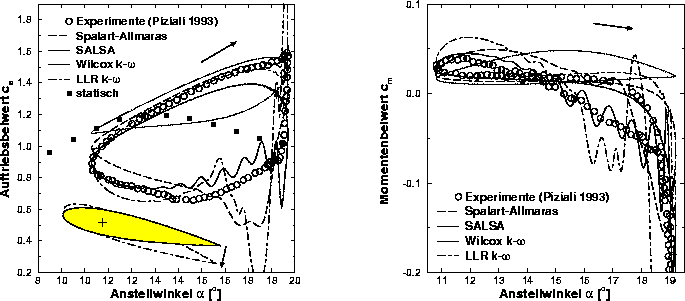
Abbildung: Auftriebsbeiwert und Momentenbeiwert
über Anstellwinkel für
Wesentlich schwieriger ist die numerische Behandlung von Bewegungen um größere Anstellwinkel. Untersucht wurde ein NACA0015 Profil bei (Abb. 2). Durch die Bewegung des Profils kann der Maximalauftrieb gegenüber dem statischen Fall bei steigendem Anstellwinkel deutlich vergrößert werden. Am Wendepunkt, wenn sich die Bewegungsrichtung umkehrt, kommt es dann allerdings zu einem plötzlichen Zusammenbruch des Auftriebs. Diese und die folgende Phase sinkenden Anstellwinkels sind von sehr komplizierten Vorgängen wie lokaler bis kompletter Strömungsablösung sowie hochfrequenter Wirbelablösung bestimmt, die von der numerischen Simulation nur qualitativ wiedergegeben werden können. Im Vergleich zu früheren Untersuchungen mit einfachen Turbulenzmodellen kann jedoch eine deutliche Verbesserung erzielt werden.