



Nächste Seite: Quellterm-Linearisierung für stets-positive Variable
Aufwärts: Quellterm-Linearisierung
Vorherige Seite: Quellterm-Linearisierung
Inhalt
- Grundregel 3 wird oft unabsichtlich verletzt.
In Zylinderkoordinaten
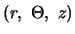 enthält die
Impulsgleichung für
enthält die
Impulsgleichung für
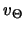 den Quellterm
den Quellterm
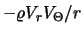 .
Man ist versucht, dies durch
.
Man ist versucht, dies durch 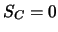 und
und
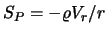 auszudrücken. Wenn jedoch
auszudrücken. Wenn jedoch 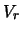 negativ wird, erhält man
negativ wird, erhält man 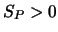 .
Eine saubere Formulierung ist
.
Eine saubere Formulierung ist
![$\displaystyle S_C = \left[\!\!\left[ {- \varrho V_r \over r},\ 0 \right]\!\!\right] V_{\Theta}$](img1020.png) und und![$\displaystyle \qquad S_P = -\left[\!\!\left[ {\varrho V_r \over r},\ 0 \right]\!\!\right] \ .$](img1021.png) |
(8.6) |
- Es ist immer möglich,
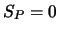 und
und 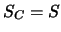 zu setzen,
was jedoch nicht wünschenswert ist. Der Effekt von stark
negativem
zu setzen,
was jedoch nicht wünschenswert ist. Der Effekt von stark
negativem 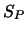 ist fast wie Unterrelaxation, was die
Konvergenz verzögert. Besser ist es, die Linie
ist fast wie Unterrelaxation, was die
Konvergenz verzögert. Besser ist es, die Linie
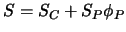 zur Tangente an die wirkliche
zur Tangente an die wirkliche
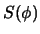 -Kurve zu machen.
-Kurve zu machen.
- Da Quellterme oft groß sind, ist es nützlich, den Extremfall
zu betrachten, wo der Quellterm alleine die
Diskretisierungsgleichung dominiert. In diesem Fall schreiben
wir
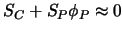 |
(8.7) |
mit der Lösung
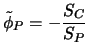 |
(8.8) |
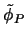 bezeichnet den Grenzwert von
bezeichnet den Grenzwert von 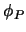 im
quellendominierten Fall.
im
quellendominierten Fall.




Nächste Seite: Quellterm-Linearisierung für stets-positive Variable
Aufwärts: Quellterm-Linearisierung
Vorherige Seite: Quellterm-Linearisierung
Inhalt
Ulf Bunge
2003-10-10
![$\displaystyle S_C = \left[\!\!\left[ {- \varrho V_r \over r},\ 0 \right]\!\!\right] V_{\Theta}$](img1020.png) und
und![$\displaystyle \qquad S_P = -\left[\!\!\left[ {\varrho V_r \over r},\ 0 \right]\!\!\right] \ .$](img1021.png)
![$\displaystyle S_C = \left[\!\!\left[ {- \varrho V_r \over r},\ 0 \right]\!\!\right] V_{\Theta}$](img1020.png) und
und![$\displaystyle \qquad S_P = -\left[\!\!\left[ {\varrho V_r \over r},\ 0 \right]\!\!\right] \ .$](img1021.png)