 |
Die in Kapitel 6.3 erläuterte Gitteranordnung mit versetzten (gestaffelten) Kontrollvolumen für die Berechnung der Geschwindigkeitskomponenten war nach ihrer Einführung in den 60er Jahren für lange Zeit der einzig bekannte Weg zur gekoppelten Berechnung von Geschwindigkeits- und Druckfeldern in inkompressiblen Strömungen. Mit versetzten Rechengittern muß jedoch ein vergrößerter Aufwand hinsichtlich des Speicherbedarfs (mehr geometrische Größen) sowie des Rechenzeitbedarfs (zusätzliche Metrikberechnungen und Interpolationen) in Kauf genommen werden. Zusätzlich steigt durch die unterschiedlichen Rechengitter auch der Programmieraufwand und die Komplexität des Rechenprogramms. Bei der Diskretisierung der Transportgleichungen in krummlinigen Koordinaten in Verbindung mit der Formulierung der Impulsgleichung in kartesischen Geschwindigkeitskomponenten können zudem Situationen auftreten, die trotz versetzter Gitter eine Entkopplung von Geschwindigkeit und Druck zur Folge haben.
Insgesamt ist festzustellen, daß viele Argumente gegen die Verwendung versetzter Rechengitter aufgezählt werden können. Eine Rechentechnik, die das Problem der Entkopplung ohne nennenswerten Mehraufwand bei Programmierung und Programmablauf sicherstellt, wurde von Rhie und Chow (1983) eingeführt. Hierauf aufbauend wurden in der Vergangenheit mehrere, im Detail unterschiedliche Wege zur Kopplung von Druck und Geschwindigkeit auf nichtversetzten (zusammenfallenden = collocated) Rechengittern vorgeschlagen. Speziell Rechenverfahren für krummlinige Koordinaten basieren seit den 80er Jahren fast ausschließlich auf nichtversetzten Gittern. Dabei wird folgende Vorgehensweise beschritten:
Zur Approximation des Druckgradiententerms in den Impulsgleichungen muß der Druck und zur Aufstellung der Massenbilanz die Geschwindigkeiten an den Kontrollvolumengrenzen ermittelt werden. Wenn Druck und Geschwindigkeit dabei linear interpoliert werden, entsteht die Gefahr, daß oszillierende Druckfelder weder in den diskretisierten Impulsgleichungen noch in der diskretisierten Kontinuitätsgleichung bemerkt werden. Bei versetzten Rechengittern wird dieses Problem dadurch umgangen, daß Geschwindigkeit und Druck an den Stellen berechnet werden, wo sie später benötigt werden. Eine Interpolation ist deshalb nicht mehr notwendig.
Eine Methode, die für nichtversetzte Gitter geeignet sein soll, muß entweder bei der Interpolation des Drucks oder bei der der Geschwindigkeit auf die Kontrollvolumengrenzen eine Kopplung zwischen Druck und Geschwindigkeit schaffen. Rhie konzentrierte sich auf die Interpolation der Geschwindigkeiten an den Kontrollvolumengrenzen, die zur Aufstellung der Massenbilanz benötigt werden.
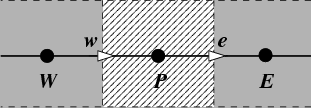
Die diskretisierte Impulsgleichung für das in Abbildung 49 skizzierte Kontrollvolumen lautet:
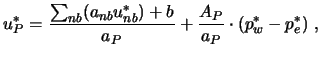
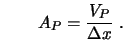
Mit den hochgestellten Indizes ![]() werden wieder die Geschwindigkeiten
gekennzeichnet, die die Impulsbilanz erfüllen.
werden wieder die Geschwindigkeiten
gekennzeichnet, die die Impulsbilanz erfüllen. ![]() und
und ![]() sind wie beim Druckkorrekturalgorithmus für gestaffelte Gitter
die Drücke, die in einer Iteration als Schätz- oder
Zwischenwerte zur Verfügung stehen (vgl. SIMPLE).
Zur Konstruktion der Interpolation werden die beiden
diskretisierten Impulsgleichungen der Punkte
sind wie beim Druckkorrekturalgorithmus für gestaffelte Gitter
die Drücke, die in einer Iteration als Schätz- oder
Zwischenwerte zur Verfügung stehen (vgl. SIMPLE).
Zur Konstruktion der Interpolation werden die beiden
diskretisierten Impulsgleichungen der Punkte ![]() und
und ![]() zu einer
Bestimmungsgleichung für die Geschwindigkeit
zu einer
Bestimmungsgleichung für die Geschwindigkeit ![]() an der
Kontrollvolumenfläche kombiniert. Die Koeffizienten, Flächen, rechten
Seiten und Druckgradienten werden dabei unter der Annahme
linear interpoliert, daß sich die Kontrollvolumengrenze in der
Mitte zwischen den Knotenpunkten befindet.
an der
Kontrollvolumenfläche kombiniert. Die Koeffizienten, Flächen, rechten
Seiten und Druckgradienten werden dabei unter der Annahme
linear interpoliert, daß sich die Kontrollvolumengrenze in der
Mitte zwischen den Knotenpunkten befindet.
Der Druck wird im Ergebnis also nicht mehr in einer Weise
interpoliert, daß sich eine Entkopplung ergeben kann, sondern
es geht vielmehr direkt der Druck an der Stelle ![]() mit in die
Gleichung ein.
mit in die
Gleichung ein.
Die obige Interpolationsvorschrift kann folgendermaßen interpretiert
werden: auf der Kontrollvolumengrenzfläche wird die Geschwindigkeit
![]() nicht als Mittelwert
der benachbarten Geschwindigkeiten
nicht als Mittelwert
der benachbarten Geschwindigkeiten ![]() und
und ![]() gebildet.
Vielmehr werden zunächst die beiden 'Pseudogeschwindigkeiten'
gebildet.
Vielmehr werden zunächst die beiden 'Pseudogeschwindigkeiten'
gemittelt. An dieser Stelle sei daran erinnert, daß die Pseudogeschwindigkeiten eine Art Impulsbilanz, die ohne Einfluß des Drucks gebildet wird, erfüllen. Zusammen mit
folgt so die Interpolationsvorschrift (6.41) zu
Das bedeutet, daß bei dem Vorschlag von Rhie die
Pseudogeschwindigkeiten ![]() anstatt der Geschwindigkeiten
anstatt der Geschwindigkeiten
![]() linear interpoliert werden und erst aus den interpolierten
Pseudogeschwindigkeiten die für die Massenbilanz
maßgeblichen Geschwindigkeiten an den Kontrollvolumengrenzen
gebildet werden. Dabei wird der Druckeinfluß wie bei SIMPLER für
versetzte Gitter überlagert.
linear interpoliert werden und erst aus den interpolierten
Pseudogeschwindigkeiten die für die Massenbilanz
maßgeblichen Geschwindigkeiten an den Kontrollvolumengrenzen
gebildet werden. Dabei wird der Druckeinfluß wie bei SIMPLER für
versetzte Gitter überlagert.
Wie bei den versetzten Rechengittern wird nun gefordert, daß durch ein entsprechendes Druckfeld die Geschwindigkeiten an den Kontrollvolumengrenzen so ermittelt werden, daß sie der Kontinuitätsgleichung genügen:
Im Gegensatz zu den versetzten Gittern soll jetzt allerdings die
Impulsbilanz mit den Geschwindigkeiten erfüllt werden, die an den
gleichen Stellen wie der Druck berechnet werden. Zum Erreichen
dieser Zielsetzung kann in Anlehnung an das weiter vorne vorgestellte
Druckkorrekturverfahren vorgegangen werden.
Hierzu wird wieder davon ausgegangen, daß die im Laufe der
iterativen Lösung gerade vorliegenden Geschwindigkeiten auf den
Kontrollvolumengrenzen ![]() und der zugehörige Druck
und der zugehörige Druck ![]() so zu
korrigieren sind, daß damit die Massenbilanz erfüllt wird.
Die Korrekturformeln lauten:
so zu
korrigieren sind, daß damit die Massenbilanz erfüllt wird.
Die Korrekturformeln lauten:
Werden nun die analog zu Gleichung (6.47) ermittelten
Geschwindigkeitskorrekturen wieder in der diskretisierten
Kontinuitätsgleichung eingesetzt, folgt eine Gleichung zur
Bestimmung der Druckkorrekturen. Diese Gleichung ist von der gleichen
Form wie die für versetzte Rechengitter. Zu beachten ist lediglich die veränderte Berechnung der Faktoren
![]() gemäß Gleichung (6.43) und die
Bestimmung des Massenfehlerterms
gemäß Gleichung (6.43) und die
Bestimmung des Massenfehlerterms ![]() mit den Geschwindigkeiten, die
wie in Gleichung (6.44) für alle
Kontrollvolumengrenzflächen zu gewinnen sind.
mit den Geschwindigkeiten, die
wie in Gleichung (6.44) für alle
Kontrollvolumengrenzflächen zu gewinnen sind.
Ausgehend von Gleichung (6.40) kann mit den
Druckkorrekturen auch eine Korrekturvorschrift für die
Geschwindigkeiten ![]() gefunden werden. Diese Korrektur ist jedoch
nicht so wesentlich für die Konvergenz des Druckkorrekturverfahrens
wie die Korrektur der Geschwindigkeiten an den Kontrollvolumengrenzen,
aus denen die neuen konvektiven Flüsse und damit die neuen
Koeffizienten der diskretisierten Impulsgleichungen errechnet
werden. Damit und mit den korrigierten Drücken folgen in der erneuten
Lösung der Impulsgleichungen bereits die zugehörigen neuen
Geschwindigkeitswerte
gefunden werden. Diese Korrektur ist jedoch
nicht so wesentlich für die Konvergenz des Druckkorrekturverfahrens
wie die Korrektur der Geschwindigkeiten an den Kontrollvolumengrenzen,
aus denen die neuen konvektiven Flüsse und damit die neuen
Koeffizienten der diskretisierten Impulsgleichungen errechnet
werden. Damit und mit den korrigierten Drücken folgen in der erneuten
Lösung der Impulsgleichungen bereits die zugehörigen neuen
Geschwindigkeitswerte ![]() an allen Kontrollvolumenzentren
an allen Kontrollvolumenzentren ![]() .
Eine zusätzliche Korrektur der Geschwindigkeiten
.
Eine zusätzliche Korrektur der Geschwindigkeiten ![]() unterstützt so allenfalls eine iterative Prozedur zur Lösung der
Impulsgleichungen, indem hierbei verbesserte Startwerte für das
Geschwindigkeitsfeld generiert werden.
unterstützt so allenfalls eine iterative Prozedur zur Lösung der
Impulsgleichungen, indem hierbei verbesserte Startwerte für das
Geschwindigkeitsfeld generiert werden.
Zusammenfassend ergibt sich für die Lösung der Navier-Stokes-Gleichungen auf nichtversetzten zweidimensionalen Gittern folgende Vorgehensweise:
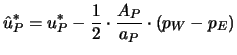 |
(6.48) |