Kontroll-Volumen-Formulierung

Die Diskretisierung einer Differentialgleichung mit Hilfe der Finite-Volumen-Methode basiert auf einem sog. Kontrollvolumen (KV) und erfolgt nach diesem Schema:

• Zerlege das Rechengebiet in KV, so daß jeder Gitterpunkt von einem KV umgeben ist.
• Integriere die Differentialgleichung über jedes KV.
• Verwende stückweise Profile für 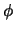$\phi$ zur Auswertung der Integrale.
• Ergebnis ist die Diskretisierungsgleichung, die 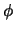$\phi$-Werte für eine Gruppe von Punkten enthält.

Die so erhaltene Diskretisierungsgleichung drückt das Erhaltungsprinzip für 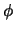$\phi$ im Kontrollvolumen aus. Daher ist für Erhaltungsgrößen wie Masse, Energie, etc. die integrale Bilanz in jedem (Teil-) Volumen erfüllt.