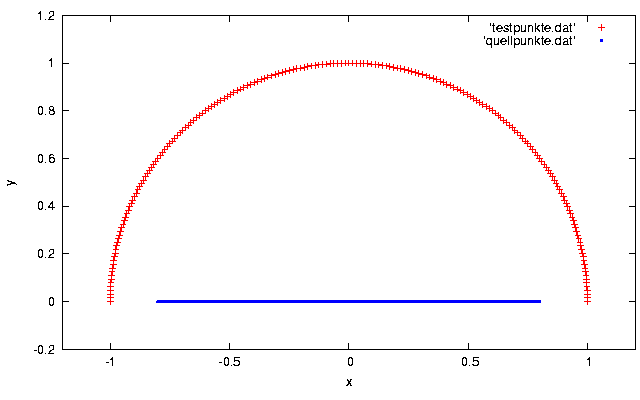
Es wird ein Beispiel gezeigt, in dem die Anzahl der Quell- und Testpunkte gleich ist. Sie beträgt 201. Das entstehende Gleichungsystem wird mit Hilfe einer Singulärwertzerlegung gelöst, obwohl eine quadratische Matrix vorliegt. Da die Kondition der entstehenden Matrix relativ groß ist, ist dieser Weg robuster. Die Wellenlaenge beträgt in dem vorgestellten Beispiel 0.588 mal den Kugelradius. Der Durchmesser der Kugel ist also mehr als drei mal groeßer als die Wellenlänge. Die ungestörte ebene Welle ist in Bild 3 dargestellt. Es ist dabei der Realteil des Feldes phi mit den in Bild 2 gezeigten Farben kodiert. Die ebene Welle in Bild 3 stellt die erste Teillösung (phi_e) des Problems dar. Diese Teillösung verletzt die Randbedingung an der Kugeloberfläche. Die Randbedingung fordert, dass die Ableitung der Lösung in Normalenrichtung verschwindet.
In Bild 4 ist die zweite Teillösung (phi_r) gezeigt. Sie ist das Feld der Ersatzquellen ohne die einfallende ebene Welle. Schließlich ist in Bild 5 die Gesamtlösung als Überlagerung der beiden Teillösungen zu sehen. Die Gesamtlösung (phi_ges = phi_e + phi_r) erfüllt die Randbedingung an der Kugeloberfläche. Die Ableitung (d phi_ges)/(d n) an der Oberfläche verschwindet jetzt.
 |
| Bild 1: Test- und Quellpunkte |
 |
| Bild 2: Farben |
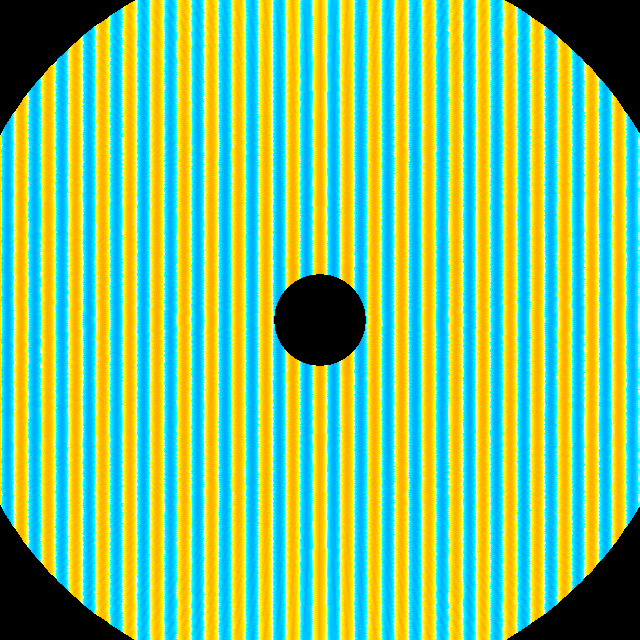 |
| Bild 3: Einfallende ebene Welle ohne Reflexion an der Kugel (phi_e) |
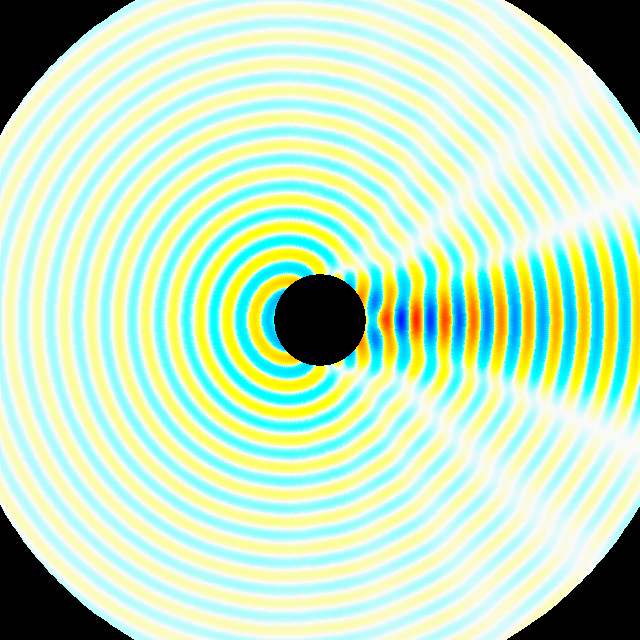 |
| Bild 4: Feld der im Zylinder sitzenden Ersatzquellen (phi_r) |
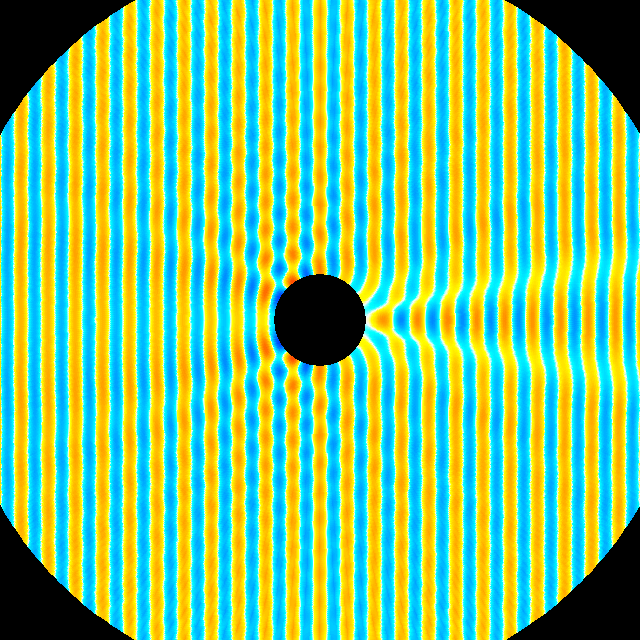 |
| Bild 5: Komplette Loesung als Ueberlagerung beider Anteile (phi_ges) |
Die beiden Programme wurden mit GNU-Octave getestet. Sie sollten aber auch mit kleinen Änderungen unter Matlab laufen. Die internen Funktionen, die bei Octave möglich sind, sollten dabei in externe Funktionen umgewandelt werden. Für die Richtigkeit der Programme wird keine Gewähr übernommen. Das Verwender der Programme geschieht auf eigene Gefahr.