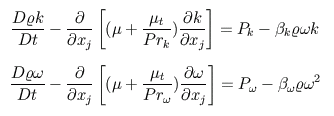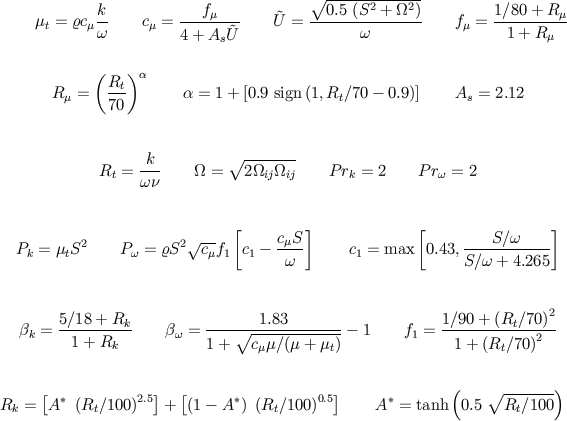The accurate prediction of complex, non-equilibrium shear flows which are close to separation whilst developing on a continuous surface is important in many fluids engineering devices operating at high-load conditions where maximum performance (e.g. pressure recovery) is obtained. In such circumstances, separation may either be provoked or suppressed in response to even slight variations in the computational representation. Hence, the predictive quality of the flow's gross characteristics may hinge on seemingly subtle modelling details in apparently innocuous flow portions. The objective of the presented LLR 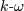model contributes to better capabilities in predicting such flows. The nature and rationale of the model are briefly outlined and results are reported in comparison to other modelling strategies.

Among the most pressing needs in the area of engineering turbulence modelling is the development of a low-Re number formulation, which facilitates a reliable description of the turbulence processes across the entire domain, including the semi-viscous near-wall regime, without the input of any ``non-local'' information, such as wall-topography parameters. Generally, the simultaneous presence of shear and severe adverse pressure gradient in the near-wall region leads to a complex, highly anisotropic turbulence structure, where the assumption that all turbulence quantities scale with the friction velocity fails, because the near-wall flow is no longer universally controlled by the wall shear-stress.

Although a general approach would, arguably, be based on full second-moment closure, which might even include a tensorial representation of dissipation, a simpler, computationally cheaper approach involving scalar turbulence quantities is defensible, provided this approach returns the correct boundary-layer structure, in particular with respect to the development of turbulent shear, and its response to adverse pressure gradient. The knowledge that the -equation is a major contributor to the misrepresentation of turbulence transport in adverse pressure gradient flows has motivated the adoption of a modified 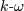variant throughout the present effort. Further motivation results from the experience that the 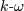frame is numerically forgiving in terms of near-wall resolution and stiffness and does not necessarily require non-local informations.

The present formulation is to a large extend in line with Shih's [3] high-Re 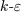approach which is based on modelling the dynamic equation for rather than . The model consists of the following governing equations:

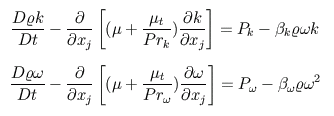
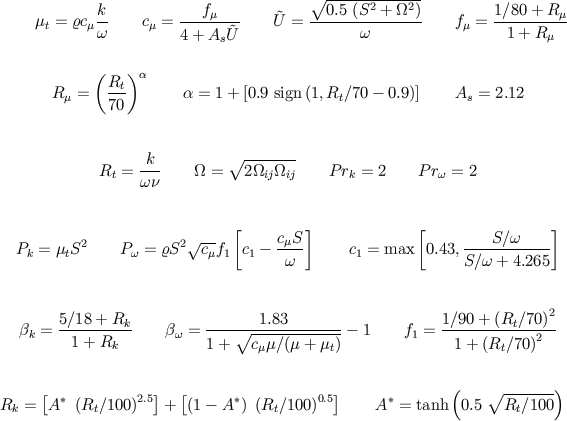
The applied low-Re number damping functions have been sensitised to the turbulence Reynolds number so as to achieve the desired asymptotic near-wall behaviour of k, and to conform with DNS data.

In order to secure realizability, the coefficient 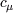must not be a constant, and must be related to mean strain and, arguably, vorticity rate [4]. This rationale is certainly also at the root of Menter's [5] shear-stress limiting ``SST'' modification of the 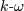model which has become increasingly popular during the last decade. However, in contrast to this, Shih's proposal, which has slightly been changed in the present formulation, applies a more sophisticated approach which tries to accomplish consistent stress-strain distributions not only in 2D plane shear flow, but also more general flow situations. Furthermore, the consideration of strain rate invariants within the Shih formulation has advantages not only with regard to realizability, but also regimes of irrotational strain, where most models tend to overestimate the turbulence production. In the following, attention is drawn to the predictive capabilities of the present LLR 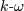model in comparison to three other low-Re eddy-viscosity models: a 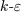model with improved predictive accuracy in adverse pressure gradient flows reported by Lien & Leschziner [6], the standard 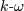model of Wilcox [7] and Menters SST 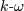model. More detailled information on the model and its rationale can be found in [1] [2].