Objectives

The aim of our research is to develop the skew symmetric scheme further to a valuable scheme for both research and engineering applications.

The skew symmetric discretization builds on rewriting the Navier-Stokes or, shown here, Euler equations in the skew symmetric form, in one dimension given by

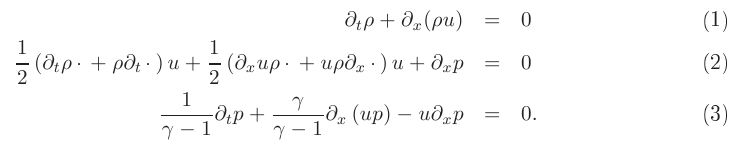
Here ρ, p, γ are density, pressure, the adiabatic index and ui (i =1,2,3) are the velocity components. The dots in the momentum equation (2) mark, that the derivatives act also on the u right of the parenthesis.
The unusual time operator in the momentum equation is a consequence of the skew symmetric rewriting of the equation.

When using skew symmetric derivative matrices it can be shown that the nonlinear transport conserves the kinetic energy in the discrete case, as in the analytical theory. This is in contrast to the majority
of numerical schemes with the exception of spectral methodes. Further the schemes used by us also conserve mass, total momentum and total energy, even though equations (2) and (3) are clearly not in
divergence form, i.e. are not equivalent to FV. The time has to be discretized carefully to keep the exact conservation. One way to do it is due to Morinishi (Morinishi, 1987) by rewriting it in (2) as

This can be discretized in time by an adopted, implicit mid-point rule, which gives a time integration scheme similar to one obtained by (Subbareddy, 2009), being fully conservative for finite time steps.
Other time integration schemes developed by us, fully and partly conservative can be derived.

Kontakt