Berechnung oszilierender Profilumströmungen


Bearbeiter:    M. Schatz,  U. Bunge,  T. Rung 

 
Ein Teil der Forschungsaktivitäten ( UNSI,  SFB557: Teilprojekt A2 ) beschäftigt sich mit der numerischen Modellierung instationäer turbulenter Strömungen auf der Basis statistischer Turbulenzmodelle. Neben der Berechnung transienter Strömunngen in  stationären Konfigurationen (Vortex Shedding past Bluff Bodies) werden auch Untersuchungen zum dynamischen Verhalten bewegter Auftriebsköper durchgeführt. Bei der hier gezeigten Anwendung handelt es sich um die Berechnung eines von Piziali vermessenen oszillierenden NACA 0015 Profils. 
 
  
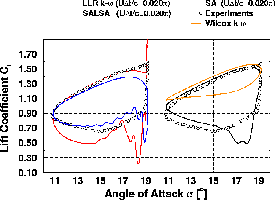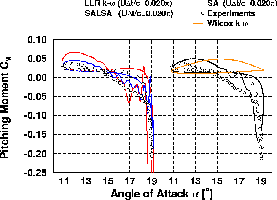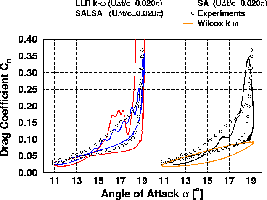
 Reynoldszahl  1.95*106
 Machzahl  0.29
 mittlerer Anstellwinkel  15o
 Anstellwinkelvariation                        4.2osin(wt)
 reduzierte Frequenz   (k=0.5wLref/Uref)  0.1
A.R. Piziali:  An experimental investigation of 2D and 3D oscillating wing aerodynamics for a range of angles of attack including stall, NASA TM 4632, 1994.
  
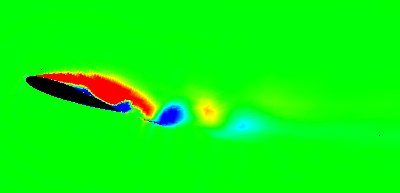
Animierte Wirbelstärkekonturen (LLR k-w und SALSA)
LLR k-w: ANIM.GIF(1.26M),  MPEG(280K),  SALSA: ANIM.GIF(560K), MPEG(5.6M), AVI(6.3M)
(In den letzten beide SALSA-Filmen wird neben den animierten Wirbelstärkekonturen noch der Auftrieb in einem animierten Diagramm gezeigt)		 mehr Informationen: 
Turbulenzmodellierung   Aerodynamik, instationär
Die Animation und die im Folgenden gezeigten Ergebnisse vermitteln einen Eindruck über die Leistungsfähigkeit linearer Wirbelzähigkeitsmodelle (SA & SALSA: Eingleichungsmodelle;  Wilcox & LLR: k-w  Zweigleichungsmodelle) für diesen Strömungstyp. Weitere Validierungsbeispiele für diese Konfiguration finden sich unter LINK. Interessant ist hierbei der Vergleich der Wirbelstärkekonturen für die beiden animierten Turbulenzmodelle. Der für die im Auftriebsspitze verantwortliche Vorderkantenwirbel hält sich beim SALSA-Modell nicht so lange wie beim LLR k-w Modell, was im stetigeren Abfall des Auftriebsbeiwertes nahe beim maximalen Anstellwinkel zu erkennen ist. Dies kann mit einer zu starken Hinterkanten-Ablösung beim SALSA-Modell im Bereich von Anstellwinkeln vor kompletter Ablösung erklärt werden.  
 
unsteady lift coefficient, 13k to load enlargement unsteady pitching moment coefficient, 13k to load enlargement unsteady drag coefficient, 13k to load enlargement
 

Webmaster

Last modified: Wed Apr 24 14:11:12 CEST 2002